例如,某大學附近的二輪電影院,發現如果票價 50 元,則大約售出 40 張票; 如果降價到票價 35 元,則可以售出 60 張票。 利用這兩個資料,估計出
那麼收入就是
從以下圖形可以看出,票價大約在 40 元左右時,達到最大收入。
R 和 p 的函數曲線圖

除了零階多項式以外,
當 x 很大的時候,多項式的值必定也很大 (或是負數,但絕對值很大)。
我們說
當 x 趨於無窮大時,
趨於無窮大或負無窮大。
也可以寫成
當,
或者
。
還可以更簡單地記做
因為當
的時候情況亦類似,所以我們可以總括地說,
任何非零階多項式
都有以下性質:
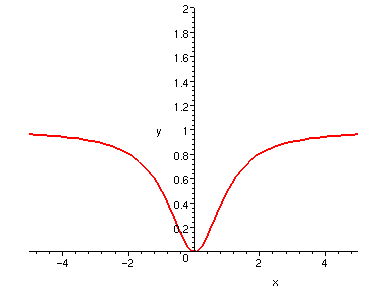
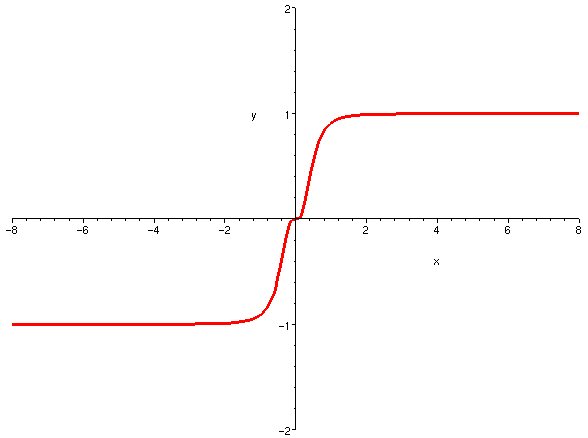
因此,以下兩條曲線都不可能是多項式函數曲線。
以上兩條函數曲線,都有水平漸近線。在符號上,兩個函數分別符合
和



關於多項式的操作技能,我們在中學都受到非常多的訓練, 現在倒是不必擔心的。以下只是提醒一些基本的事實。
- 多項式等式
以下,我們觀察兩個多項式函數曲線。
| y = -4*x^3 + 28*x - 24 | y = x^4 - 15*x^2 - 15*x |
|---|---|

| 
|
當 x 趨於無窮大時,
也可以寫成
當
還可以更簡單地記做
因為當
因此,以下兩條曲線都不可能是多項式函數曲線。
| 
|
和
多項式函數曲線一定是連續的。所以,以下曲線不可能是多項式的函數曲線。

在座標平面上給 n + 1 個點(這些點不違背函數曲線的要求),
則必定有一個、而且僅有一個、n 階多項式的函數曲線通過這 n + 1 個點。
同理,如果兩個 n 階多項式在 n + 1 個點上相等,
那麼這兩個多項式就完全相同。
例如,只有一個二階多項式會通過 (-1, 1), (0, 0), (1, 1) 這三個點,
因此,以下三條曲線,雖然都通過那三點,但是只有一條是二階多項式。

習題
- 題目
- a 和 b 是兩個實數。若 c = a + b i
是多項式
的一個根,證明 必定有一個二階因式 - 若一個公司估計某產品的獲利 R 是單價 p 的函數:
請問在單價多少的時候獲利最多?此時獲利多少?- 根據物理定律,從地面向上拋出物體,此物的高度 s (拋出點當作 0,以公尺計) 是時間 t (拋出時當作 0,以秒計) 的多項式函數:
其中 g 是引力常數,v0 是拋出時的速度, 也稱為 初速度 (initial velocity)。請回答以下問題。- 多久以後此物會落回到高度 s = 0 處。
- 它最高能夠到達幾公尺?
- 若一個公司估計某產品的獲利 R 是單價 p 的函數: