基底 (basis) - 向量空間的重點

我們先來複習一些名詞:
若 v1， v2，...， vn V， 且 vi 0， i = 1，2，...，n
如果我們說 v1， v2 ，...， vn " 線性相關 "， 意思就是:
a1， a2， ...， an 不全為零 s.t. a1v1 + a2v2 + ... + a2v2 = 0

如果我們說 v1， v2 ，...， vn " 線性無關 "， 意思就是:
a1， a2， ...， an 不全為零 s.t. a1 v1 + a2 v2 + ... + a2 v2 = 0

也就是說， a1 v1 + a2 v2 + ... + an vn = 0 a1=a2=...=an=0.

在 上， 平行的直線就是線性相關， 不平行的直線就是線性無關. 而 " 空間的維度 " 就是最多線性無關的向量個數.

接下來我們要介紹 " 基底 ":
若v1，v2，...，vn V 是 V 的一組基底， 意思就是說:

  1. 它是最大個數的線性無關的向量集合.
  2. v V
    係數 ( 純量 ) ， ，...， s.t. v = . v1， . v2，...， . vn
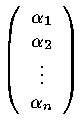
    此時我們稱 是 v 在此基底下的向量表達
    ( 同樣的向量， 在不同的基底下， 會有不同的 " 向量表達 ".)

注意， 和 V 要區分清楚， 是一個向量空間， 但向量空間 V 不一定是 。 舉例來說， V = span{1, x, x 2,x 3} span {1，x-1，(x-1)2， (x-1)3}

V

= span {1，x，x2，x3} =
v= 3x3 - 2x2 + x - 1= + (x-1) + (x-1)2 + (x-1)3
= p' + p'( x - 1 ) + p''(x - 1 )2 +p'''3 (x - 1 )3
此即為 v 在"1" 那一點作泰勒展開
= =

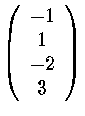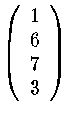
對於向量表達， 我們舉個平面上的例子:
在基底 (1，0)，(0，1) 時的向量 (1，1)， 和
在基底 ( ，)， (， ) 時的向量 (1，0)，
和在基底 (1，0)，(0，-1) 時的向量 (1，-1)， 指的都是同一個向量.
這裡要注意的是: 向量在不同基底的意義之下， 有不同的表達， 而矩陣亦同。矩陣是線性映射的表達， 所有的矩陣運算都只是在換基底罷了。

以下要介紹一些不同特性的基底:

basis ( 基底 )

: 最大個數的線性無關的向量集合

正交基底

:是基底並且兩兩互相垂直

正則基底

: 是兩兩互相垂直的基底並且長度均為 1
( 這是我們最喜歡的基底 )

和其它種類的基底比較起來， 正則基底能夠使 v = . v1 + . v2有唯一一組 的計算， 而且在求向量表達時也較容易:

以下我們來針對這些不同的基底做個練習:
若 x，y 表示 (1，0)，(0，1) 這組標準基底， 令 v1 = ， v2 = ， 而 v = 。
此時，v = v1 + v2， 所以我們以 v 來表示它。很明顯的，

= . =3 1

= = 2 1

所以我們引進 dual basis ( 對偶基底 ) ， ， 使得 v = + 找尋 的過程如下:
使 同時符合

< ，v1 > = 1 <， v1 > = 0
< ，v2 > = 1 <， v2 > = 1

此時， = = ${-1\choose 1}_{\{\mbox{\boldmath$x$ }，\mbox{\boldmath$y$ }\}}$

則 v = <v， $\tilde{\mbox{\boldmath$v$ }}_1$>_ {x，y}.$\tilde{v}$