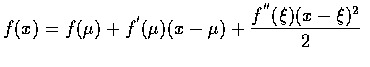Other Inequalities

Proposition (One-Sided Chebyshev Inequality)
If X is a random variable with mean 0 and finite variance $\sigma^2$, then for any a>0

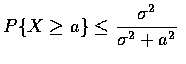
$P\{X\geq a\}\leq\displaystyle\frac{\sigma^2}{\sigma^2+a^2}$
Proof:
Let b>0 and note that
$X\geq a$ is equivalent to $X+b\geq a+b$
Hence
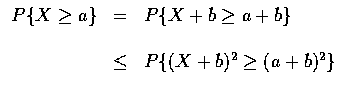
$\begin{array}{rcl} P\{X\geq a\}&=&P\{X+b\geq a+b\} \\ \\ &\leq&P\{(X+b)^2\geq(a+b)^2\} \end{array}$
where the above inequality is obtained by noting that, since a+b>0, $X+b\geq a+b$ implies that $(X+b)^2\geq(a+b)^2$. Upon applying Markov's inequality, the above yield that
$P\{X\geq a\}\leq\displaystyle\frac{E[X+b)^2]}{(a+b)^2}=\frac{\sigma^2+b^2}{(a+b)^2}$
Letting $b=\sigma^2/a$ [which is easily seen to be the value of b that minimizes $(\sigma^2+b^2)/(a^2+b^2)$] gives the desired result.          $\rule[0.02em]{1.0mm}{1.5mm}$

Suppose now that X has mean $\mu$ and variance $\sigma^2$. As both $X-\mu$and $\mu-X$ have mean 0 and variance $\sigma^2$, we obtain, from the one-sided Chebyshev inequality, that for a>0,

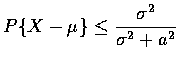
$P\{X-\mu\geqa\}&\leq&\displaystyle\frac{\sigma^2}{\sigma^2+a^2}$
and
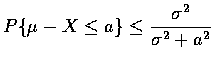
$P\{\mu-X\leq a\}&\leq&\displaystyle\frac{\sigma^2}{\sigma^2+a^2}$
Thus we have the following corollary.

Corollary
If $E[X]=\mu$, $Var(X)=\sigma^2$, then for a>0,

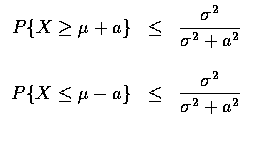
$\begin{array}{rcl} P\{X\geq\mu+a\}&\leq&\displaystyle\frac{\sigma^2}{\sigma^2+a... ...X\leq\mu-a\}&\leq&\displaystyle\frac{\sigma^2}{\sigma^2+a^2} \\ \\ \end{array}$

When the moment generating function of the random variable X is known, we can obtain even more effective bounds on $P\{X\geq a\}$. Let M(t)=E[etX] be the moment generating function of the random variable X. Then for t>0,

$\begin{array}{rcl} P\{X\leq a\}&=&P\{e^{tX}\geq e^{ta}\} \\ \\ &\leq&E[e^{tX}]e^{-ta} \end{array}$
Thus we have the following inequalities, known as Chernoff bounds.

Proposition (Chernoff Bounds)

$P\{X\geq a\}\leq e^{-ta}M(t)\qquad\mbox{ for all } t>0$
$P\{X\leq a\}\leq e^{-ta}M(t)\qquad\mbox{ for all } t<0$
Since the Chernoff bounds hold for all t in either the positive or negative quadrant, we obtain the best bound on $P\{X\geq a\}$ by using the t that minimizes e-taM(t).

Definition
A twice-differentiable real-valued function f(x) is said to be convex if $f^{''}\geq 0$ for all x; similarly, it is said to be concave if $f^{''}\leq 0$
Some examples of convex functions are f(x)=x2, f(x)=eax, f(x)=-x1/nfor $x\geq 0$. If f(x) is convex, then g(x)=-f(x) is concave, and vice versa.

Proposition (Jensen's Inequality)
If f(x) is a convex function, then

$E[f(X)]\geq f(E[X])$
provided that the expectations exist and are finite.
Proof:
Expanding f(x) in a Taylor's series expansion about $\mu=E[X]$ yields
$f(x)=f(\mu)+f^{'}(\mu)(x-\mu)+\displaystyle\frac{f^{''}(\xi)(x-\xi)^2}{2}$
where $\xi$ is some value between x and $\mu$. Since $f^{''}(\xi)\geq 0$ we obtain
$f(x)\geq f(\mu)+f^{'}(\mu)(x-\mu)$
Hence
$f(X)\geq f(\mu)+f^{'}(\mu)(X-\mu)$
Taking expectations yields
$E[f(X)]\geq f(\mu)+f^{'}(\mu)E[X-\mu]=f(\mu)\qquad\rule[0.02em]{1.0mm}{1.5mm}$