Chebyshev's Inequality and Weak Law of Large Numbers

Proposition (Markov's Inequality)
If X is a random variable that takes only nonnegative values, then any value a>0

$\displaystyle P\{X\geq a\}\leq\frac{E[X]}{a}$
Proof:
For a>0 let
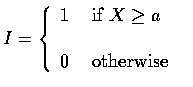
$I=\left\{ \begin{array}{ll} 1&\mbox{ if } X\geq a \\ \\ 0&\mbox{ otherwise } \end{array}\right .$
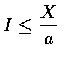and note that, since $X\geq 0$, $\displaystyle I\leq\frac{X}{a}$. Taking expectations of the above yields that
$E[I]\leq\displaystyle\frac{E[X]}{a}$
which, since $E[I]=P\{X\geq a\}\qquad\rule[0.02em]{1.0mm}{1.5mm}$

Proposition (Chebyshev's Inequality)
If X is a random variable with finite mean $\mu$ and variance $\sigma^2$, then for any value k>0

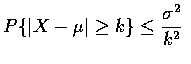
$P\{\vert X-\mu\vert\geq k\}\leq\displaystyle\frac{\sigma^2}{k^2}$
Proof:
Since $(X-\mu)^2$ is a nonnegative random variable, we can apply Markov's inequality (with a=k2) to obtain
$P\{(X-\mu)^2\geq k^2\}\leq\displaystyle\frac{E[(X-\mu)^2]}{k^2}\qquad (2.1)$
But since $(X-\mu)^2\geq k^2$ if and only if $\vert X-\mu\vert\geq k$, then (2.1) is equivalent to
$P\{\vert X-\mu\vert\geq k\}\leq\displaystyle\frac{E[(X-\mu)^2]}{k^2}=\frac{\sigma^2}{k^2} \qquad\rule[0.02em]{1.0mm}{1.5mm}$

Proposition
If Var(X)=0, then $P\{X=E[X]\}=1$.
In other words, the only random variables having variances equal to 0 are those that are constant with probability 1.
Proof: By Chebyshev's inequality we have, for any $n\geq 1$

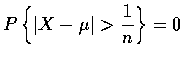
$P\left\{\vert X-\mu\vert>\displaystyle\frac{1}{n}\right\}=0$
Letting $n\rightarrow\infty$ and using the continuity property of probability yields
$\begin{array}{rcl} 0=\displaystyle\lim_{n\rightarrow\infty}P\left\{\vert X-\mu\... ...\}\right\} \\ \\ &=&P\{X\neq\mu\}\qquad\rule[0.02em]{1.0mm}{1.5mm} \end{array}$

Theorem (The Weak Law of Large Numbers)
Let $X_1,X_2,\ldots$ be a sequence of independent and identically distributed random variables, each having finite mean $E[X_i]=\mu$. Then, for any $\varepsilon>0$,

$P\left\{\left \vert\displaystyle\frac{X_1+\cdots+X_n}{n}-\mu\right \vert\geq\varepsilon\right\} \rightarrow 0$
as $n\rightarrow\infty$
Proof:
We shall prove the result only under the additional assumption that the random variables have a finite variance $\sigma^2$. Now, as $E\left [\displaystyle\frac{X_1+\cdots+X_n}{n}\right ]=\mu$ and $Var\left (\displaystyle\frac{X_1+\cdots+X_n}{n}\right )=\frac{\sigma^2}{n}$it follows from Chebyshev's inequality that
$P\left\{\left \vert\displaystyle\frac{X_1+\cdots+X_n}{n}-\mu\right \vert\geq\va... ...on\right\} \leq\frac{\sigma^2}{n\varepsilon^2}\qquad\rule[0.02em]{1.0mm}{1.5mm}$