Additional Properties of Normal Random Variables

The Multivariate Normal Distribution
Let $Z_1,\ldots,Z_n$ be a set of n independent unit normal random variables. If, for some constants aij, $1\leq i\leq m$, $1\leq j\leq m$, and $\mu_i$, $1\leq i\leq m$,

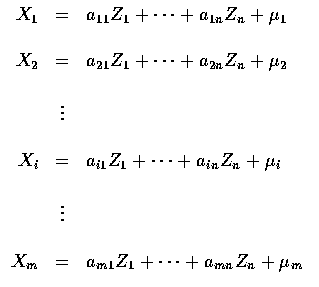
$\begin{array}{rcl} X_1&=&a_{11}Z_1+\cdots+a_{1n}Z_n+\mu_1 \\ \\ X_2&=&a_{21}Z_... ...\mu_i \\ \\ &\vdots& \\ \\ X_m&=&a_{m1}Z_1+\cdots+a_{mn}Z_n+\mu_m \end{array}$
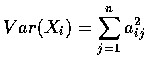then the random variables $X_1,\ldots,X_m$ are siad to have a multivariate normal distribution. And for each Xi have $E[X_i]=\mu_i$, $Var(X_i)=\displaystyle\sum_{j=1}^na_{ij}^2$. And then consider
$M(t_1,\ldots,t_m)=E[\exp\{t_1X_1+\cdots+t_mX_m\}]$
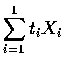the joint M.G.F. of $X_1,\ldots,X_m$. Since $\displaystyle\sum_{i=1}^1t_iX_i$ is itself a linear combination of the independent normal random variables $Z_1,\ldots,Z_n$, it is also normally distributed. So
$E\left [\displaystyle\sum_{i=1}^mt_iX_i\right ]=\sum_{i=1}^mt_i\mu_i$
and
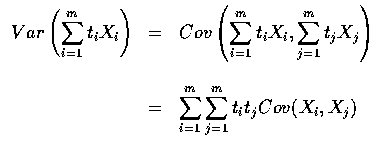
$\begin{array}{rcl} Var\left (\displaystyle\sum_{i=1}^mt_iX_i\right )&=& Cov\lef... ...) \\ \\ &=&\displaystyle\sum_{i=1}^m\sum_{j=1}^mt_it_jCov(X_i,X_j) \end{array}$
Thus the joint M.G.F
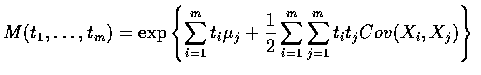
$M(t_1,\ldots,t_m)=\exp\left\{\displaystyle\sum_{i=1}^mt_i\mu_j+ \frac{1}{2}\sum_{i=1}^m\sum_{j=1}^mt_it_jCov(X_i,X_j)\right\}$

Proposition
If $X_1,\ldots,X_n$ are independent are identically distributed normal random variables with mean $\mu$ and variance $\sigma^2$, then the sample mean $\overline{X}$ and the sample variance S2/(n-1) are independent. $\overline{X}$ is a normal random variable with mean $\mu$ and variance $\sigma^2/m$; $S^2/\sigma^2$ is a chi-squared random variable with n-1 degrees of freedom.