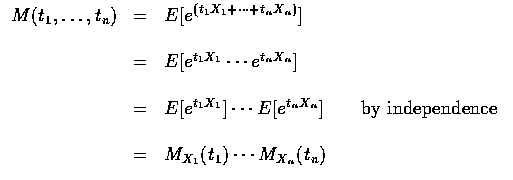Property of Moment Generating Function

An important property of moment generating functions is that the moment generating function of the sum of independent random variables equals the product of the individual moment generating functions. To prove this, suppose that X and Y are independent and have moment generating functions MX(t)and MY(t), respectively. Then MX+Y(t), the moment generating function of X+Y, is given by

$\begin{array}{rcl} M_{X+Y}&=&E[e^{t(X+Y)}] \\ \\ &=&E[e^{tX}e^{tY}] \\ \\ &=&E[e^{tX}]E[e^{tY}] \\ \\ &=&M_X(t)M_Y(t) \end{array}$
since X and Y are independent. Another important result is that the moment generating function uniquely determines the distribution. That is, MX(t)exists and is finite in some region about t=0, then the distribution of X is uniquely determined.


It is also possible to define the joint moment generating function of two or more random variables. This is done as follows. For any n random variables $X_1,\ldots,X_n$, the joint moment generating function, $M(t_1,\ldots,t_n)$, is defined for all real values of $t_1,\ldots,t_n$ by

$M(t_1,\ldots,t_n)=E[e^{t_1X_1+\cdots+t_nX_n}]$
The individul moment generating functions can be obtained from $M(t_1,\ldots,t_n)$ by letting all but one of the tj be 0. That is,
$M_{X_i}(t)=E[e^{tX_i}]=M(0,\ldots,0,t,0,\ldots,0)$
where the t is in the ith place.

It can be proved (although the proof is too advanced for this text) that $M(t_1,\ldots,t_n)$ uniquely determines the joint distribution of $X_1,\ldots,X_n$. This result can then be used to prove that the n random variables $X_1,\ldots,X_n$ are independent if and only if

$M(t_1,\ldots,t_n)=M_{X_1}(t_1)\cdots M_{X_n}(t_n)\qquad (6.4)$
This follows because, if the n random variables ae independent, then
$\begin{array}{rcl} M(t_1,\ldots,t_n)&=&E[\displaystyle e^{(t_1X_1+\cdots+t_nX_n... ...ad \mbox{by independence} \\ \\ &=&M_{X_1}(t_1)\cdots M_{X_n}(t_n) \end{array}$
On the other hand, if Equation (6.4) is satisfied, then the joint moment generating function $M(t_1,\ldots,t_n)$ is the same as the joint moment generating function of n independent random variables, the ith of which has the same distribution of Xi. As the joint moment generating function uniquely determines the joint distribution, this must be the joint distribution; hence the random variables are independent.