Conditional Variance
就如同在定義給予 Y 值後, X 的條件期望值一樣, 我們也可以定義在給予 Y=y後 X 的 條件變異數 (conditional varianec). 其定義如下:
Var(X|Y) = E[[X-E(X|Y)]2|Y]
也就是說, 當 Y 的值給定後, Var(X|Y) 為 X與它的(條件)期望值之差的平方的(條件)期望值. 換句話說,
Var(X|Y) 與通常之變異數的定義是類似的, 唯一的差別是所有的期望值是在 Y已知的條件下求得的.
X 的無條件變異數 Var(X) 和給予 Y 後 X 的條件變異數 Var (X|Y)間存在著一個非常有用的關係式, 此關係式經常被用來求 Var(X). 欲得此關係式,
首先我們注意到基於與
Var (X) = E[X2] - (E[X])2 同樣的理由, 我們有
Var(X|Y) = E[X2|Y] - (E[X|Y])2
所以
又因為
E[E[X|Y]] = E[X], 我們得
Var(E[X|Y]) = E[(E[X|Y])2] - (E[X])2
Proposition (The conditional Variance Formula)
Var(X) = E [ Var (X|Y)] + Var(E[X|Y])
- Example
- 假設到任意時間 t, 抵達車站的人數為均數是
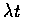 的卜瓦松隨機變數.
假設第一班火車到達車站的時間 (與旅客何時到站無關) 在區間 (0,T)
上均勻分布, 試求進入火車的旅客人數的平均數和變異數.
的卜瓦松隨機變數.
假設第一班火車到達車站的時間 (與旅客何時到站無關) 在區間 (0,T)
上均勻分布, 試求進入火車的旅客人數的平均數和變異數.
- Solution:
- 對任意
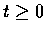 ,
令 N(t) 表示到時間 t 時抵達車站的人數, 且令 Y表示火車到站的時間. 則我們感興趣的隨機變數為 N(Y). 以 Y 為條件, 得
by the independence of Y and N(t) since N(t) is Poisson with mean
,
令 N(t) 表示到時間 t 時抵達車站的人數, 且令 Y表示火車到站的時間. 則我們感興趣的隨機變數為 N(Y). 以 Y 為條件, 得
by the independence of Y and N(t) since N(t) is Poisson with mean
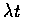
因此
![$ E[N(Y)\vert Y] = \lambda Y$](img5.gif) 取期望值得
取期望值得
![$E[N(Y)] = \lambda E[Y] = \displaystyle\frac{\lambda T}{2}$](img6.gif) 欲求 Var(N(t)), 我們利用條件變異數公式:
欲求 Var(N(t)), 我們利用條件變異數公式:
所以
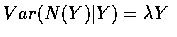 ,
,
![$ E[N(Y)\vert Y] = \lambda Y$](img5.gif) 因此 ,由條件變異數公式得
其中我們利用了
因此 ,由條件變異數公式得
其中我們利用了
![$Var(Y) = \displaystyle\frac{T^2}{12}\qquad\rule[0.02em]{1.0mm}{1.5mm}$](img10.gif)
- Example (Variance of a Random Number of Random Variables)
- Let
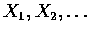 be a sequence of independent and identically distributed
random variables and let N be a nonnegative integer valued random variable
that is independent of the sequence
be a sequence of independent and identically distributed
random variables and let N be a nonnegative integer valued random variable
that is independent of the sequence
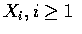 .
To compute
.
To compute
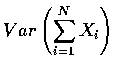 ,
we condition on N:
The above follows, since given
,
we condition on N:
The above follows, since given
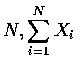 is just the sum of a
fixed number of independent random variables, so its expectation and variance
is just the sum of the individual means and variances. Hence, from the
conditional variance formula,
is just the sum of a
fixed number of independent random variables, so its expectation and variance
is just the sum of the individual means and variances. Hence, from the
conditional variance formula,
![$\begin{array}{rcl}
E[Var(X\vert Y)]&=&E[E[X^2\vert Y]] - E[(E[X\vert Y])^2] \\ \\
&=&E[X^2] - E[(E[X\vert Y])^2]
\end{array}$](img1.gif)
![$\begin{array}{rcl}
E[Var(X\vert Y)]&=&E[E[X^2\vert Y]] - E[(E[X\vert Y])^2] \\ \\
&=&E[X^2] - E[(E[X\vert Y])^2]
\end{array}$](img1.gif)
![$\begin{array}{rcl}
E[N(Y)\vert Y=t] & = & E[N(t)\vert Y=t] \\ \\
& = & E[N(t)] \\ \\
& = & \lambda t
\end{array}$](img4.gif)
![]() 取期望值得
取期望值得
![$E[N(Y)] = \lambda E[Y] = \displaystyle\frac{\lambda T}{2}$](img6.gif) 欲求 Var(N(t)), 我們利用條件變異數公式:
欲求 Var(N(t)), 我們利用條件變異數公式:
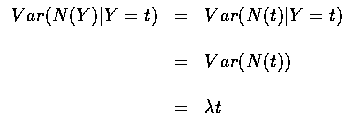
![$\begin{array}{rcl}
Var(N(Y)) & = & E[\lambda Y] + Var(\lambda Y) \\ \\
& = & \displaystyle\lambda \frac{T}{2} + \lambda ^2 \frac{T^2}{12}
\end{array}$](img9.gif)
![$Var(Y) = \displaystyle\frac{T^2}{12}\qquad\rule[0.02em]{1.0mm}{1.5mm}$](img10.gif)
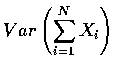 ,
we condition on N:
,
we condition on N:
![$\begin{array}{rcl}
E\left [\displaystyle\sum_{i=1}^N X_i\vert N\right ]&=&NE[X]...
...\
Var\left (\displaystyle\sum_{i=1}^N X_i\vert N\right )&=&NVar(X)
\end{array}$](img15.gif)
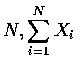 is just the sum of a
fixed number of independent random variables, so its expectation and variance
is just the sum of the individual means and variances. Hence, from the
conditional variance formula,
is just the sum of a
fixed number of independent random variables, so its expectation and variance
is just the sum of the individual means and variances. Hence, from the
conditional variance formula,
![$Var\left (\displaystyle\sum_{i=1}^N X_i\right )=E[N]Var(X)+(E[X])^2Var(N)\qquad\rule[0.02em]{1.0mm}{1.5mm}$](img17.gif)