Computing Probabilities by Conditioning
我們不只可利用條件期望值來求一隨機變數的期望值,
同時亦可用同樣的方法求得有關的機率. 欲達此目的,
設 E 為任一事件且定義指標隨機變數 X 如下:
則由 X 的定義得
因此,
值得一提的是, 當 Y 為離散隨機變數, 且所有可能值為
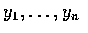 時,
若定義事件 Fi 如下:
時,
若定義事件 Fi 如下:
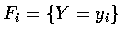 ,
,
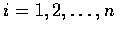 則 (4.8) 式就是我們所熟悉的等式
其中,
則 (4.8) 式就是我們所熟悉的等式
其中,
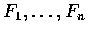 為聯集是樣本空間的互斥事件.
為聯集是樣本空間的互斥事件.
- Example
- 設 X 和 Y 為獨立的連續隨機變數. 求 X+Y 的分布.
- Solution:
- 以 Y 的值為條件, 得
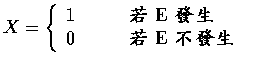
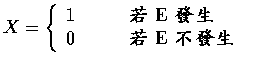
![$\begin{array}{rcl}
E[X]&=&P(E) \\ \\
E[X\vert Y=y]&=&P (E\vert Y=y) \qquad \mbox{對任意隨機變數} Y
\end{array}$](img2.gif)
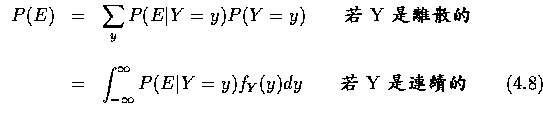
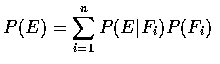
![$\begin{array}{rcl}
P\{ X+Y< a\}&=&\displaystyle\int_{-\infty}^\infty P\{X+Y\leq...
...nfty}^\infty F_X (a-y) f_Y (y) dy \qquad\rule[0.02em]{1.0mm}{1.5mm}
\end{array}$](img9.gif)