Computing Expectations by Conditioning
我們以 E[X|Y] 表示隨機變數 Y 的函數, 它在 Y=y 的值為條件期望值 E[X|Y=y].
注意到 E[X|Y] 本身即為一隨機變數, 所以可以求它的期望值.
下面的 Proposition 是有關條件期望值的一個非常重要的性質.
Proposition
E[X] = E[ E[X|Y] ]
當 Y 為離散隨機變數時, 上式為
![$ E[X] = \displaystyle\sum_y E[X\vert Y=y] P\{Y=y \} $](img1.gif)
而當 Y 為連續隨機變數且密度函數為 fY(y) 時, 則為
![$ E[X] = \displaystyle\int_{-\infty}^\infty E[X\vert Y=y]f_Y(y)dy $](img2.gif)
Proof:
下面我們只證明 X 和 Y 都是離散隨機變數的情形.
(X 和 Y 都是離散的情形): 我們必須證明
因 (4.2) 式右邊可寫成
了解 (4.2) 式的一種方法是將它作如下的解釋 : 欲求 E[X], 我們求在 Y=y的條件下, X 之條件期望值的加權平均值, 其中每一項 E[X|Y=y]的權數為該項所給之條件事件的機率. 這是一個非常有用的結果,
因為經常可藉著對某一變數取條件期望值而容易地求得所需的期望值.
我們以下面的一些例子來說明它的用處.
- Example (Expectation of a Random Number of Random Variables
- 假設在某一天進入某一百貨公司的人數為一期望值是 50 的隨機變數,
且有共同的期望值 $8. 又假設每一顧客所花的錢和進入此百貨公司的總人數亦是獨立的.
試求某一天內顧客們在此百貨公司所花的總錢數的期望值.
- Solution:
- 設 N 表示進入此百貨公司的總人數, Xi 表示第 i 位顧客所花的錢數,
則顧客們所花的總錢數可表示成
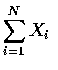 .
因
又
故得
.
因
又
故得
![$E \left [ \displaystyle\sum_{i=1}^N X_i \Big \vert N \right ] = NE[X]$](img8.gif) 所以
因此在本例中, 進入此百貨公司之顧客們所花的總錢數的期望值為
所以
因此在本例中, 進入此百貨公司之顧客們所花的總錢數的期望值為
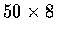 ,
即
$400.
,
即
$400.
![$\rule[0.02em]{1.0mm}{1.5mm}$](img11.gif)
- Example
- 設
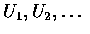 為一獨立的均勻 (0,1) 隨機變數序列. 求 E[N], 其中
為一獨立的均勻 (0,1) 隨機變數序列. 求 E[N], 其中
- Solution:
- 我們解下述較一般的結果, 而本例即為其一特例. 對
![$ x \in [0,1] $](img15.gif) ,
令
且設
m(x) = E[N(x)]也就是說, N(x) 是總和首次超過 x 所需之均勻 (0,1) 隨機變數的個數,
而 m(x) 為其期望數. 我們將以 U1 為條件導出 m(x) 的表示式. 故有
因
當 y>x 時, 前一個公式是很明顯的. 當
,
令
且設
m(x) = E[N(x)]也就是說, N(x) 是總和首次超過 x 所需之均勻 (0,1) 隨機變數的個數,
而 m(x) 為其期望數. 我們將以 U1 為條件導出 m(x) 的表示式. 故有
因
當 y>x 時, 前一個公式是很明顯的. 當  時, 第二個式子是對的,
因為若第一個均勻隨機變數的值為 y,
則此時剩餘的均勻隨機變數的個數與一開始時所需相加直到其和超過 x-y之均勻隨機變數的個數是一樣的. 將 (4.7) 式代入 (4.6) 式得
將上式微分得
m' (x) = m(x) 亦即
時, 第二個式子是對的,
因為若第一個均勻隨機變數的值為 y,
則此時剩餘的均勻隨機變數的個數與一開始時所需相加直到其和超過 x-y之均勻隨機變數的個數是一樣的. 將 (4.7) 式代入 (4.6) 式得
將上式微分得
m' (x) = m(x) 亦即
 積分得
積分得
![$\log [m(x)] = x + c $](img22.gif) 即
m(x) = kex
即
m(x) = kex
因 m(x) =1, 故得 k=1, 所以我們得到
m(x) = ex所以, 總和首次超過 1 所需之均勻 (0,1) 隨機變數的期望數 m(1) 等於
![$e\qquad\rule[0.02em]{1.0mm}{1.5mm}$](img23.gif) .
.
![$ E[X] = \displaystyle\sum_y E[X\vert Y =y] P\{Y =y\} \qquad (4.2)$](img3.gif)
![$ E[X] = \displaystyle\sum_y E[X\vert Y=y] P\{Y=y \} $](img1.gif)
![$ E[X] = \displaystyle\int_{-\infty}^\infty E[X\vert Y=y]f_Y(y)dy $](img2.gif)
![$ E[X] = \displaystyle\sum_y E[X\vert Y =y] P\{Y =y\} \qquad (4.2)$](img3.gif)
![$ \begin{array}{rcl}
\displaystyle\sum_y E[X\vert Y=y]P\{Y=y\}&=&\displaystyle\s...
... xP\{ X=x \} \\ \\
&=&E[X] \qquad\qquad\rule[0.02em]{1.0mm}{1.5mm}
\end{array}$](img4.gif)
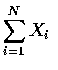 .
因
.
因
![$E\left [\displaystyle\sum_{i=1}^N X_i \right ] =
E \left [ E \left [ \sum_{i=1}^N X_i \Big \vert N \right ] \right ] $](img6.gif)
![$\begin{array}{rcl}
E\left [ \displaystyle\sum_{i=1}^N X_i \Big \vert N=n \right...
...box{ and } N \\ \\
& = & nE[X] \qquad \mbox{ where } E[X] = E[X_i]
\end{array}$](img7.gif)
![$E \left [ \displaystyle\sum_{i=1}^N X_i \Big \vert N \right ] = NE[X]$](img8.gif) 所以
所以
![$ E \left [ \displaystyle\sum_{i=1}^N x_i \right ] = E [NE[X]] = E[N]E[X]$](img9.gif)
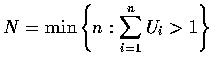
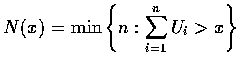
![$ m(x) = \displaystyle\int_0^1 E[N(x) \vert U_1 =y ] fy \qquad (4.6)$](img17.gif)
![$ E[N(x) \vert U_1 = y ] = \left \{
\begin{array}{ll}
1 & \mbox{ if } y > x \\
1 + m(x-y) & \mbox{ if } y \leq x \qquad (4.7)
\end{array} \right .$](img18.gif)
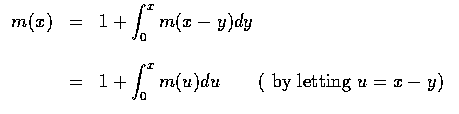
 積分得
積分得
![]() .
.