Conditional Expectation
設 X 和 Y 為聯合離散隨機變數, 那麼在已知 Y=y 的條件下, X 的條件機率
質量函數的定義為
其中
pY (y) > 0. 因此我們很自然的作如下的定義: 對所有滿足
pY (y) > 0 的
y, 定義在 Y=y 的條件下, X 的 條件期望值 (conditional expectation) 為
同樣, 設 X 和 Y 為聯合連續隨機變數, 其聯合機率密度函數為 f(x,y),
那麼對所有滿足
fY (y) > 0 的 y, 在已知 Y=y 的條件下,
X 的條件機率密度函數的定義為
因此, 當
fY (y) > 0 時, 很自然地定義在 Y=y 的條件下, X 的條件期望值為
- Example
- 設 X 和 Y 的聯合密度函數為
求 E[X|Y=y].
- Solution:
- 我們先求條件密度函數
因此, 給予 Y=y, X 的條件分布恰為期望值是 y 的指數分布. 故得
Remark
Just as conditional probabilities satisfy all of the properties of ordinary
probabilities, so do conditional expectations satisfy the properties of
ordinary expectations. For instance, such formulas as
and
remain valid. As a matter of fact, conditional expectation given Y=y can be
thought of as being an ordinary expectation on a reduced sample space consisting
only of outcomes for which Y=y.
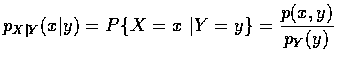
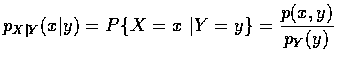
![$\begin{array}{rcl}
E[X\vert Y=y]&=&\displaystyle\sum_x P\{ X=x\vert Y=y \}\\ \\
&=&\displaystyle\sum_x xp_{X\vert Y} (x\vert y)
\end{array}$](img2.gif)
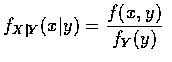
![$ E[X\vert Y=y] = \displaystyle\int_{-\infty}^\infty xf_{X\vert Y} (x\vert y) dx $](img4.gif)
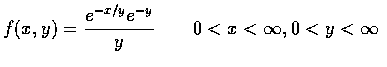
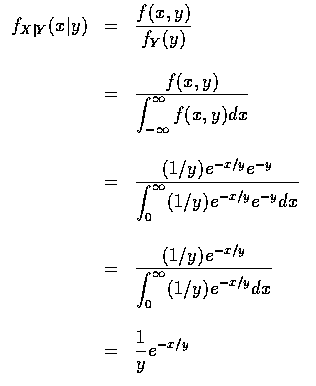
![$ E[X\vert Y=y] = \displaystyle\int_0^\infty \frac{x}{y} e^{-x/y} dx = y $](img7.gif)
![$E[g(X)\vert Y=y]=\left\{
\begin{array}{ll}
\displaystyle\sum_x g(x)p_{X\vert Y}...
...x)f_{X\vert Y}(x\vert y)dx&\mbox{ in the continuous case }
\end{array}\right .$](img9.gif)
![$E\left [\displaystyle\sum_{i=1}^n X_i\vert Y=y\right ]=\displaystyle\sum_{i=1}^n E[X_i\vert Y=y]$](img10.gif)