Correlation

Proposition
The correlationof two random variables X and Y, denoted by $\rho (X,Y)$, is defined, as long as Var(X) Var(Y) is positive, by

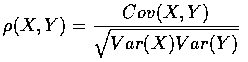
$\rho(X,Y)=\displaystyle\frac{Cov(X,Y)}{\sqrt{Var(X)Var(Y)}}$
It can be shown that $-1\leq\rho(X,Y)\leq 1$
Solution:
Suppose that X and Y have variances given by $\sigma_x^2$ and $\sigma_y^2$, respectively. Then
$\begin{array}{rcl} 0&\leq&Var\left (\displaystyle\frac{X}{\sigma_x}+\frac{Y}{\s... ...a_y^2}+ \frac{2Cov(X,Y)}{\sigma_x\sigma_y} \\ \\ &=&2[1+\rho(X,Y)] \end{array}$
implying that $-1\leq\rho(X,Y)\qquad\rule[0.02em]{1.0mm}{1.5mm}$


In fact, since Var(Z)=0 implies that Z is constant with probability 1, we see that $\rho(X,Y)=1$ implies that Y=a+bX, where $b=\sigma_x/\sigma_y>0$ and $\rho(X,Y)=-1$ implies that Y=a+bX, where $b=-\sigma_y/\sigma_x<0$.

If Y=a+bX, then $\rho (X,Y)$ is either +1 or -1, depending on the sign of b.

The correlation coefficient is a measure of the degree of linearity between Xand Y. A value of $\rho (X,Y)$ near +1 or -1 indicates a high degree of linearity between X and Y, whereas a value near 0 indicates a lack of such linearity. A positive value of $\rho(X,Y)=0$, then X and Y are said to be uncorrelated

Example
Let IA and IB be indicator variables for the events A and B. That is,
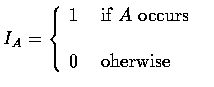
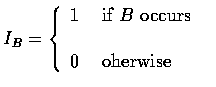
$I_A=\left\{ \begin{array}{ll} 1&\mbox{ if }A\mbox{ occurs } \\ \\ 0&\mbox{ oherwise } \end{array}\right .$ $I_B=\left\{ \begin{array}{ll} 1&\mbox{ if }B\mbox{ occurs } \\ \\ 0&\mbox{ oherwise } \end{array}\right .$
Then E[IA]=P(A), E[IB]=P(B), E[IAIB]=P(AB) so
$\begin{array}{rcl} Cov(I_A,I_B)&=&P(AB)-P(A)P(B) \\ \\ &+&P(B)[P(A\vert B)-P(A)] \end{array}$
Thus we obtain the quite intuitive result that the indicator variables for Aand B are either positively correlated, uncorrelated, or negatively correlated depending on whether P(A|B) is greater than, equal to, or less than $P(A)\qquad\rule[0.02em]{1.0mm}{1.5mm}$

Example
Let $X_1,\ldots,X_n$ be independent and identically distributed random variables having variance $\sigma^2$. Show that $Cov(X_i-\overline{X},\overline{X})=0$
Solution:
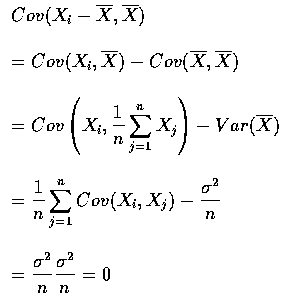
$\begin{array}{ll} Cov(X_i-\overline{X},\overline{X}) \\ \\ =Cov(X_i,\overline{... ...a^2}{n} \\ \\ =\displaystyle\frac{\sigma^2}{n}\frac{\sigma^2}{n}=0 \end{array}$
the final equality follows since
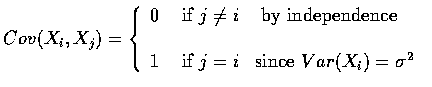
$Cov(X_i,X_j)=\left\{ \begin{array}{lll} 0&\mbox{ if } j\neq i&\mbox{ by indepen... ... } \\ \\ 1&\mbox{ if } j=i&\mbox{since } Var(X_i)=\sigma^2 \end{array}\right .$

Although $\overline{X}$ and the deviation $X_i-\overline{X}$ are uncorrelated, they are not, in general, independent. However, in the special case where the Xi are normal random variables it turns out that not only is $\overline{X}$independent of a single deviation but it is independent of the entire sequence of deviations $X_j-\overline{X}, j=1,\ldots,n$. The sample mean $\overline{X}$and the sample variance S2/(n-1) are independent with $S^2/\sigma^2$ haveing a chi-squared distribution with n-1 degrees of freedom.