
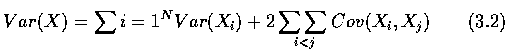
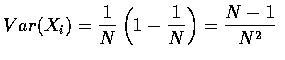
Cov(Xi,Xj)=E[XiXj]-E[Xi]E[Xj]
Now,

![$\begin{array}{rcl}
E[X_iX_j]&=&P\{X_i=1,X_j=1\} \\ \\
&=&P\{X_i=1\}P\{X_j=1\vert X_i=1\} \\ \\
&=&\displaystyle\frac{1}{N}\frac{1}{N-1}
\end{array}$](img7.gif)
Hence,
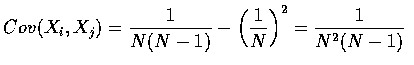
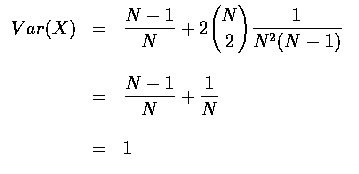
Problem

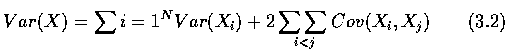
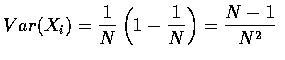

![$\begin{array}{rcl}
E[X_iX_j]&=&P\{X_i=1,X_j=1\} \\ \\
&=&P\{X_i=1\}P\{X_j=1\vert X_i=1\} \\ \\
&=&\displaystyle\frac{1}{N}\frac{1}{N-1}
\end{array}$](img7.gif)
Hence,
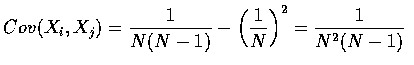
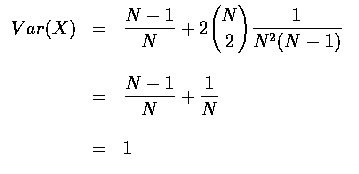
Thus both the mean and variance of the number of matches are equal to 1. When
N is large, the probability of i matches is approximately e-1/i!. That
is, when N is large, the number of matches is approximately distributed as a
Poisson random variable with mean 1. Hence, as the mean and variance of a
Poisson random variable are equal.