Example
- Example
- 設
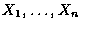 為獨立且有相同分布的隨機變數, 其期望值為
為獨立且有相同分布的隨機變數, 其期望值為 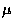 ,
變異數為
,
變異數為 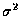 ,
且令
,
且令
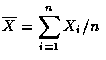 為樣本均數.
為樣本均數.
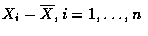 ,稱為 離差 (deviation),
因為它們是每一個別資料和樣本均數的差. 令 S2 表示這些離差的平方和.
也就是說,
隨機變數 S2/(n-1) 稱為 樣本變異數 (sample variance).
求 (a)
,稱為 離差 (deviation),
因為它們是每一個別資料和樣本均數的差. 令 S2 表示這些離差的平方和.
也就是說,
隨機變數 S2/(n-1) 稱為 樣本變異數 (sample variance).
求 (a)
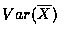 ,
和 (b)
E[S2 /(n-1)].
,
和 (b)
E[S2 /(n-1)].
- Solution:
- (a)
(b)
將上式兩邊取期望值得
其中最後一個等式利用 (a) 的結果. 將兩邊除以 n-1,
得樣本變異數的期望值就是分布變異數
![$\sigma ^2\qquad\rule[0.02em]{1.0mm}{1.5mm}$](img11.gif) .
.
- Example (Variance of a Binomial Random Variable)
- Compute the variance of a binomial random variable X with parameters n and
p.
- Solution:
- Since such a random variable represents the number of successes in nindependent trials when each trial has a common probability p of being a
success, we may write
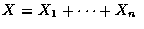 where the Xi are independent
Bernoulli random variables such that
Hence, we have
where the Xi are independent
Bernoulli random variables such that
Hence, we have
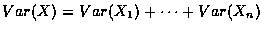 .
But
and thus
.
But
and thus
![$Var(X)=np(1-p)\qquad\rule[0.02em]{1.0mm}{1.5mm}$](img17.gif)
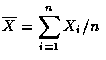 為樣本均數.
為樣本均數.
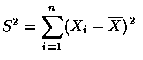
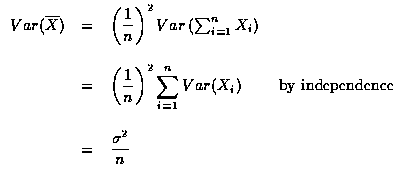
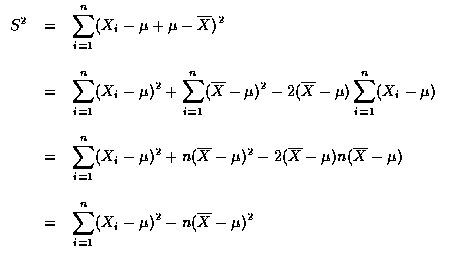
![$\begin{array}{rcl}
E[S^2]&=&\displaystyle\sum_{i=1}^n E [(X_i - \mu)^2] - nE[(\...
... \\
&=& n \sigma ^2 - nVar(\overline{X}) \\ \\
&=& (n-1)\sigma ^2
\end{array}$](img10.gif)
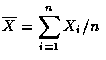 為樣本均數.
為樣本均數.
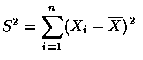
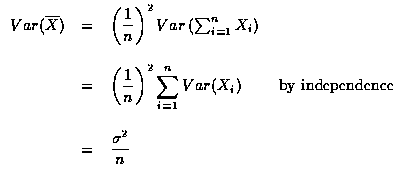
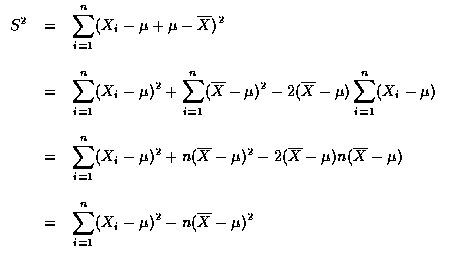
![$\begin{array}{rcl}
E[S^2]&=&\displaystyle\sum_{i=1}^n E [(X_i - \mu)^2] - nE[(\...
... \\
&=& n \sigma ^2 - nVar(\overline{X}) \\ \\
&=& (n-1)\sigma ^2
\end{array}$](img10.gif)

![$\begin{array}{rcl}
Var(X_i)&=&E[X_i^2]-(E[X_i])^2 \\ \\
&=&E[X_i]-(E[X_i])^2 \qquad \mbox{since} X_i^2=X_i \\ \\
&=&p-p^2
\end{array}$](img16.gif)