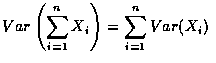Covariance, Variance of Sums

Proposition
設 X 和 Y 為獨立隨機變數, 則對任意函數 h 和 g E[ g(X)h(Y) ] = E[g(X)]E[h(Y)]
Proof:
假設 X 和 Y 為聯合連續隨機變數, 其聯合密度函數為 f(x,y). 則

$\begin{array}{rcl} E[g(X)h(Y)] & = & \displaystyle\int_{-\infty}^\infty \int_{-... ... (x)dx \\ \\ & = & E [h(Y)Eg(X)] \qquad\rule[0.02em]{1.0mm}{1.5mm} \end{array}$
離散情形的證明是相同的.


就如同單一隨機變數的期望值和變異數提供我們有關該隨機變數的訊息一樣, 兩隨機變數間的互變異數(covarianec) 也提供我們有關隨機變數間之關係的訊息.

Definition
隨機變數 X 和 Y 間的互變異數, 以符號 Cov(X,Y) 表示, 定義為 Cov(X,Y) = E[ (X-E[X])(Y-E[Y]) ]


將上述定義中之右邊展開, 我們得

$\begin{array}{rcl} Cov(X,Y) & = & E[ XY -E[X]Y - XE[Y] + E[Y]E[X] ] \\ \\ & = & E[XY] - E[X]E[Y] - E[X]E[Y] + E[X]E[Y] \\ \\ & = & E[XY] - E[X]E[Y] \end{array}$
當 X 和 Y 獨立時, 由上面的 Proposition 得 Cov(X,Y)=0. 但其逆敘述是不對的. 兩相依隨機變數 X 和 Y 有零互變異術的一個簡單的例子如下: 令 X 為一隨機變數, 其機率質量函數為
$ P\{X=0\} = P \{X=1\} = P\{ X=-1\} = \displaystyle\frac{1}{3} $
定義
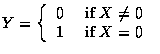
$ Y = \left \{ \begin{array}{ll} 0 & \mbox{ if } X \neq 0 \\ 1 & \mbox{ if } X = 0 \end{array} \right .$
則 XY=0, 所以 E[XY] = 0. 又 E[X]=0, 故
cov(X,Y) = E[XY] - E[X]E[Y] = 0
但很顯然的, X 和 Y 並不為獨立隨機變數.


Proposition

(i)
Cov(X,Y) = Cov(Y,X)
(ii)
Cov(X,X) = Var(X)
(iii)
Cov(aX,Y) = a Cov(X,Y)
(iv)
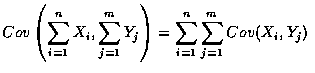
$Cov \left ( \displaystyle\sum_{i=1}^n X_i, \sum_{j=1}^m Y_j \right ) = \displaystyle\sum_{i=1}^n\sum_{j=1}^m Cov(X_i,Y_j)$
Proof:
(iv)
部份說明互變異數運算具有加法性 (就如同期望值的運算一樣), 欲證此部分, 我們令 $\mu _i = E[X_i], \nu _j = E[Y_j] $. 則
$E \left [ \displaystyle\sum_{i=1}^n X_i \right ] = \sum_{i=1}^n \mu _i$ $E\left [ \displaystyle\sum_{j=1}^m Y_j \right ] = \displaystyle\sum_{j=1}^m \nu _j$
且
$\begin{array}{l} Cov \left ( \displaystyle\sum_{i=1}^n X_i, \sum_{j=1}^m Y_j \r... ...^m E[(X_i-\mu _i)(Y_j - \nu _j) ] \qquad\rule[0.02em]{1.0mm}{1.5mm} \end{array}$
其中最後一個等式是因為隨機變數之和的期望值等於期望值之和的緣故.


在上個 Proposition 中 (2) 和 (4), 令 $Y_j = X_j, j=1,2,\ldots,n$, 則得

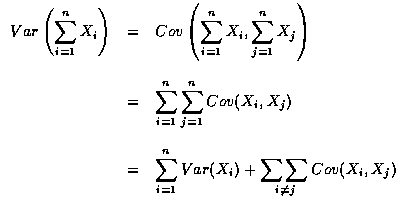
$\begin{array}{rcl} Var\left ( \displaystyle\sum_{i=1}^n X_i \right ) & = & Cov ... ...}^n Var(X_i) + \sum\sum_{\hspace{-0.5cm}i \neq j} Cov (X_i,X_j) \\ \end{array}$
因每一對不相等的足標 i,j (即 $i \neq j$), 在二重求和中均出現兩次, 故上述等 式相當於:

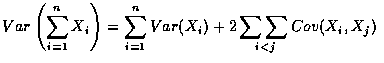
$Var \left ( \displaystyle\sum_{i=1}^n X_i \right ) = \displaystyle\sum_{i=1}^n Var(X_i)+ 2 \sum\sum_{\hspace{-0.5cm}i < j} Cov (X_i,X_j) $

若 $X_1,\ldots,X_n$ 為 成對獨立 (pairwise independent), 亦即當 $i \neq j$時, Xi 和 Xj 為獨立隨機變數, 則上式變成

$ Var \left ( \displaystyle\sum_{i=1}^n X_i \right ) = \displaystyle\sum_{i=1}^n Var (X_i) $