Problem　III

When one is dealing with an infinite collection of random variables $X_i,i\geq 1$, each having a finite expectation, it is not necessarily true that

$E\left [\displaystyle\sum_{i=1}^\infty X_i\right ] = \sum_{i=1}^\infty E[X_i]\qquad (2.3)$
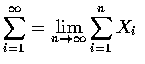To determine when (2.3) is valid, we note that $\displaystyle\sum_{i=1}^\infty=\lim_{n\rightarrow\infty}\sum_{i=1}^n X_i$and thus
$\begin{array}{rcl} E\left [\displaystyle\sum{i=1}^\infty X_i\right ]&=& E\left ... ...}\sum_{i=1}^nE[X_i] \\ \\ &=&\displaystyle\sum_{i=1}^\infty E[X_i] \end{array}$

Hence Equation (2.3) is valid whenever we are justified in interchanging the expectation and limit operations in Equation (2.4). Although, in general, this interchange is not justified, it can be shown to be valid in two important special cases:

1.
The Xi are all nonnegative random variables (that is, $P\{X_i\geq 0\}=1$for all i).
2.
$\displaystyle\sum_{i=1}^\infty E[\vert X_i\vert]<\infty$

Example
Consider any nonegative, integer-valued random variable X. If we define,for each $i\geq 1$,
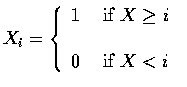
$X_i=\left\{ \begin{array}{ll} 1&\mbox{ if }X\geq i \\ \\ 0&\mbox{ if }X<i \end{array}\right .$
then
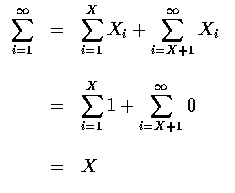
$\begin{array}{rcl} \displaystyle\sum_{i=1}^\infty&=&\displaystyle\sum_{i=1}^X X... ...\ &=&\displaystyle\sum_{i=1}^X 1+\sum_{i=X+1}^\infty 0 \\ \\ &=&X \end{array}$
Hence, since the Xi are all nonnegative,
$\begin{array}{rcl} E[X]&=&\displaystyle\sum_{i=1}^\infty E(X_i) \\ \\ &=&\displaystyle\sum_{i=1}^\infty P\{X\geq i\} \end{array}$

If X is a nonnegative continuous random variable and $P\{X\geq 0\}=1$. Then $E[X]=\displaystyle\int_0^\infty P\{Y\geq y\}dy\qquad\rule[0.02em]{1.0mm}{1.5mm}$.