Problem II
- Example (A random Walk in the Plane)
- 平面上的 隨機漫步 (random walk). 考慮一質點剛開始時是在平面上某一定點,
假設它歷經一系列定'長的步程, 但方向是完全隨機的. 特別地,
假設每步之後的新位置與前一位置的距離為 1 各單位長, 且與前一位置之方向角在區間
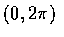 上均勻分布 (如圖所示). 試求 n 步之後與原點之距離平方的期望值.
上均勻分布 (如圖所示). 試求 n 步之後與原點之距離平方的期望值.
- Solution:
- 令
(Xi, Yi) 表示在第 i 步的位置變化量 (以直角坐標表示),
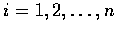 .
則我們有
.
則我們有
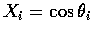 ,
,
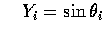 其中
其中
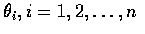 .
根據假設為獨立且在
.
根據假設為獨立且在 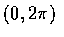 上的均勻分布的隨機變數. 因 n 步後之位置的直角坐標為
上的均勻分布的隨機變數. 因 n 步後之位置的直角坐標為
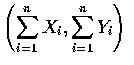 ,
故知從原點到該位置之距離的平方 D2 為
其中我們用了
,
故知從原點到該位置之距離的平方 D2 為
其中我們用了
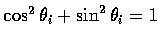 的結果. 當然
的結果. 當然
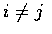 時,
時, 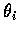 和
和 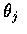 為獨立隨機變數, 又
因此對上式之兩邊取期望值得
為獨立隨機變數, 又
因此對上式之兩邊取期望值得
![$E[D^2]= n \qquad\rule[0.02em]{1.0mm}{1.5mm}$](img13.gif)
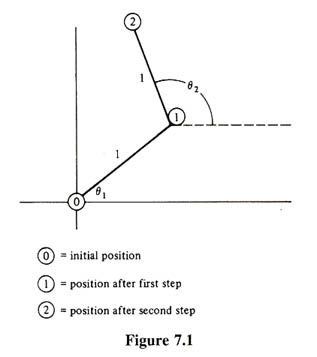
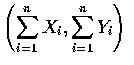 ,
故知從原點到該位置之距離的平方 D2 為
,
故知從原點到該位置之距離的平方 D2 為
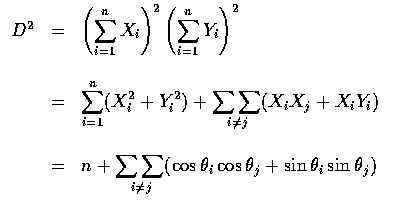
![$\begin{array}{rcl}
E[\cos\theta_i]&=&\displaystyle\int_0^{2\pi}\cos udu=\sin 2\...
...in\theta_i]&=&\displaystyle\int_0^{2\pi}\sin udu=\cos 0-\cos 2\pi=0
\end{array}$](img12.gif)

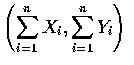 ,
故知從原點到該位置之距離的平方 D2 為
,
故知從原點到該位置之距離的平方 D2 為
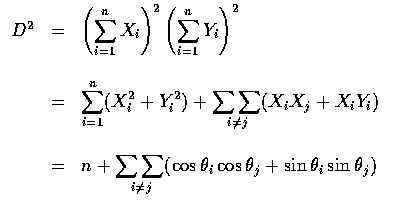
![$\begin{array}{rcl}
E[\cos\theta_i]&=&\displaystyle\int_0^{2\pi}\cos udu=\sin 2\...
...in\theta_i]&=&\displaystyle\int_0^{2\pi}\sin udu=\cos 0-\cos 2\pi=0
\end{array}$](img12.gif)