Proposition
有關二維的隨機變數之函數的期望值, 我們假設 X 和 Y 為隨機變數, g 為一兩
個變數的函數, 則我們有下面的結果.
Proposition
若 X 和 Y 的聯合機率質量函數為 p(x,y), 則
若 X 和 Y 的聯合機率密度函數為 f(x,y), 則
- Example
- 意外發生的地點 X 均勻分布在一長為 L 的路上. 意外發生的時候,
救護車所在的位置 Y 也是均勻分布在該路上. 假設 X 和 Y 為獨立隨機變數,
試求救護車與意外地點間的期望距離.
- Solution:
- 我們欲求
E[| X-Y |]. 因為 X 和 Y 的聯合密度函數為
由上面的 Proposition 得
由
所以
關於上面的 Proposition 的一個重要應用, 我們假設 E[X] 和 E[Y] 都是有限且令
g(X,Y) = X+Y. 則在連續的情形我們得到
在一般的情形下, 也可得到同樣的結果; 因此, 當 E[X] 和 E[Y] 為有限時,
E[X+Y] = E[X] + E[Y]
And, using a simple induction proof shows that if E[Xi] is finite for all
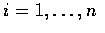 then
then
is an extremely useful formula whose utility will now be illustrated by a series
of examples.
![$E[g(X,Y)] = \displaystyle\sum_y \sum_x g(x,y)p(x,y)$](img1.gif)
![$E[g(X,Y)] = \displaystyle\sum_y \sum_x g(x,y)p(x,y)$](img1.gif)
![$E[g(x,y)]=\displaystyle\int_{-\infty}^\infty\int_{-\infty}^\infty g(x,y)f(x,y)dxdy$](img2.gif)
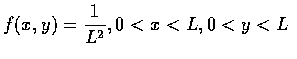
![$ E[\vert X-Y \vert] = \displaystyle\frac{1}{L^2} \int_0^L \int_0^L \vert x-y\vert dy dx$](img4.gif)
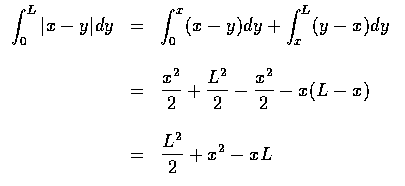
![$\begin{array}{rcl}
E[\vert X-Y \vert]&=&\displaystyle\frac{1}{L^2}\int_0^L\left (\frac{L^2}{2}+x^2-xL\right )dx\\ \\
&=&\displaystyle\frac{L}{3}
\end{array}$](img6.gif)
![$ \begin{array}{rcl}
E[X+Y]&=&\displaystyle\int_{-\infty}^\infty\int_{-\infty}^\...
... xf_x (x) dx+\int_{-\infty}^\infty yf_Y(y)dy \\ \\
&=& E[X] + E[Y]
\end{array}$](img8.gif)
![]() then
then