Introduction

在本章中我們將導出且應用期望值的其他性質. 首先, 讓我們回憶一下期望值的定義: 當 X 為離散隨機變數,其機率質量函數為 p(x) 時, 隨機變數 X 的期望值定義為

$E[X] = \displaystyle\sum_x xp(x) $
當 X 為連續隨機變數其機率密度函數為 f(x) 時, 其期望值的定義為
$E[X] = \displaystyle\int_{-\infty}^\infty xf(x)dx $
因 E[X] 為 X 之所有可能值的加權平均, 故當 X 的值必須介於 a 與 b 之間時, 則其期望值也必介於 a 與 b 之間 . 也就是說, 當
$ P\{a \leq X \leq b \} =1 $
時, 則
$ a \leq E[X] \leq b $
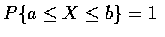欲證上述的結果, 我們假設 X 為一離散隨機變數且 $ P\{a \leq X \leq b \} =1 $. 因為此假設導致對所有在區間 [a,b] 外的 x, p(x) = 0, 故得
$ \begin{array}{rcl} E[X] = \displaystyle\sum_{x:p(x)>0} xp(x) & \geq & \display... ...(x) \\ \\ & = & a \displaystyle\sum_{x:p(x)>0} p(x) \\ \\ & = & a \end{array}$
同樣的方法可證得 $E[X] \leq b$, 所以上述的結果對離散隨機變數而言是對的. 又連續情形的證明也是一樣的, 故得欲證的結果.