Joint Probability Distribution Function on n-dimention

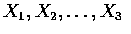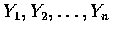When the joint density function of the n random variables $X_1,X_2,\ldots ,X_3$ is given and we want to compute the joint density function of $Y_1,Y_2,\ldots ,Y_n$, where

$Y_1=g_1(X_1,\ldots,X_n)$, $Y_2=g_2(X_1,\ldots,X_n)$,..., $Y_n=g_n(X_1,\ldots,X_n)$
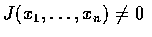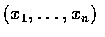the aproach is the same. Namely, we assume that the functions gi have continuous partial derivatives and that the Jacobian determinant $J(x_1,\ldots,x_n)\neq 0$ at all points $(x_1,\ldots,x_n)$, where
$J(x_1,\ldots,x_n)=\left \vert \begin{array}{cccc} \displaystyle\frac{\partial g... ... \cdots& \displaystyle\frac{\partial g_n}{\partial x_n} \end{array}\right \vert$
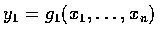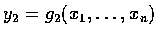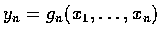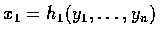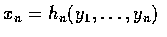Furthermore, we suppose that the equations $y_1=g_1(x_1,\ldots,x_n)$, $y_2=g_2(x_1,\ldots,x_n)$,..., $y_n=g_n(x_1,\ldots,x_n)$ have a unique solution, say, $x_1=h_1(y_1,\ldots,y_n)$,..., $x_n=h_n(y_1,\ldots,y_n)$Under these assumptions the joint density function of the random variables Yi is given by
$f_{Y_1,\ldots,Y_n}(y_1,\ldots,y_n)= f_{X_1,\ldots,X_n}(x_1,\ldots,x_n)\vert J(x_1,\ldots,x_n)\vert^{-1}$
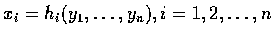
where $x_i=h_i(y_1,\ldots,y_n), i=1,2,\ldots,n$

Example
設 X1, X2, X3 為獨立的標準常態隨機變數. 若 Y1 = X1 + X2 + X3, Y2 = X1 - X2, Y3 = X1 - X3, 試求 Y1, Y2, Y3 的聯合密度函數.
Solution:
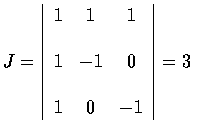
令 Y1 = X1 + X2 + X3, Y2 = X1 - X2, Y3 = X1 - X3, 則這些變換的 Jacobian 行列式為
$ J = \left \vert \begin{array}{ccc} 1 & 1 & 1 \\ \\ 1 & -1 & 0 \\ \\ 1 & 0 & -1 \end{array} \right \vert = 3 $
又由上述變換得
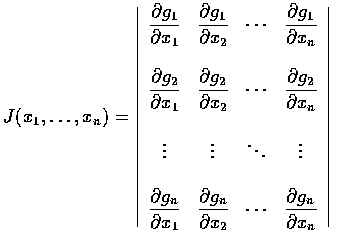
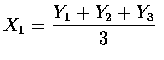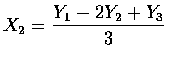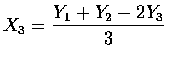
$ X_1 = \displaystyle\frac{Y_1+Y_2+Y_3}{3}$, $X_2 = \displaystyle\frac{Y_1 - 2Y_2 + Y_3}{3}$, $X_3 = \displaystyle\frac{Y_1+Y_2-2Y_3}{3}$
所以我們得
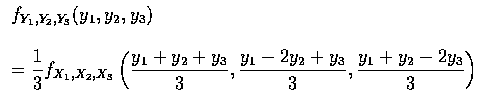
$\begin{array}{l} f_{Y_1,Y_2,Y_3} (y_1,y_2,y_3) \\ \\ =\displaystyle\frac{1}{3}... ...2+y_3}{3},\frac{y_1-2y_2 + y_3}{3}, \frac{y_1+y_2-2y_3}{3} \right ) \end{array}$

因此,

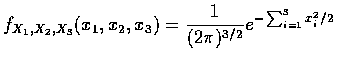
$f_{X_1,X_2,X_3}(x_1,x_2,x_3)=\displaystyle\frac{1}{(2\pi)^{3/2}} e^{-\sum_{i=1}^3 x_i^2/2}$
故得
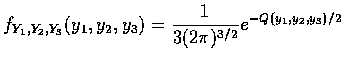
$f_{Y_1,Y_2,Y_3}(y_1,y_2,y_3)=\displaystyle\frac{1}{3(2\pi)^{3/2}} e^{-Q(y_1,y_2,y_3)/2}$
其中,
$\begin{array}{l} Q(y_1,y_2,y_3) \\ \\ =\displaystyle\left (\frac{y_1+y_2+y_3}{... ...frac{2}{3}y_3^2- \frac{2}{3}y_2y_3\qquad\rule[0.02em]{1.0mm}{1.5mm} \end{array}$