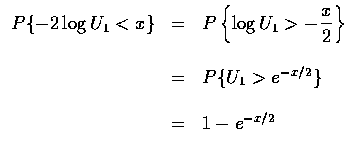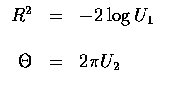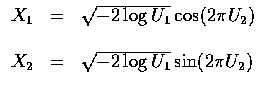Let (X,Y) denote a random point in the plane and assume that the rectangular
coordinates X and Y are independent unit normal random variables. We are
interested in the joint distribution of 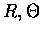 ,
the polar coordinate
representation of this point. as follow,
,
the polar coordinate
representation of this point. as follow,
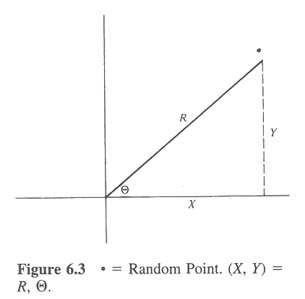
Letting
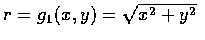 and
and
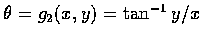 ,
we see
that
,
we see
that
Hence
As the joint density function of X and Y is
we see that joint density function of
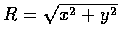 ,
,
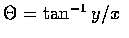 ,
is given by
As this joint density factors into the marginal densities for
,
is given by
As this joint density factors into the marginal densities for 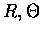 ,
we obtain that
,
we obtain that 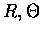 are independent random variables, with
are independent random variables, with 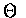 being uniformly distributed over
being uniformly distributed over 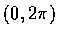 and R having the Rayleigh
distribution with density
and R having the Rayleigh
distribution with density
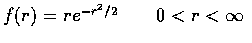 (Thus, for
instance, when one is aiming at a target in the plane, if the horizontal and
vertical miss distances are independent unit normals, then the absolue value of
the error has the above Rayleigh distribution.)
(Thus, for
instance, when one is aiming at a target in the plane, if the horizontal and
vertical miss distances are independent unit normals, then the absolue value of
the error has the above Rayleigh distribution.)
The above result is quite interesting, for it certainly is not evident a priori
that a random vector whose coordinates ae independent unit normal random
variables will have an angle of orientation that is not only uniformly
distributed, but is also independent of the vector's distance from the origin.
If we wanted the joint distribution of
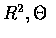 ,
then, as the
transformation
d=g1(x,y)=x2+y2 and
,
then, as the
transformation
d=g1(x,y)=x2+y2 and
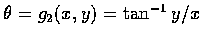 has a
Jacobian
has a
Jacobian
we see that
Therefore,
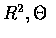 are independent, with R2 having an exponential
distribution with parameter
are independent, with R2 having an exponential
distribution with parameter
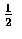 .
But as
R2=X2+Y2, it follow,
by definition, that R2 has a chi-squared distribution with 2 degrees
of freedom. Hence we have a verification of the result that the exponential
distribution with parameter
.
But as
R2=X2+Y2, it follow,
by definition, that R2 has a chi-squared distribution with 2 degrees
of freedom. Hence we have a verification of the result that the exponential
distribution with parameter
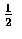 is the same as the chi-squared
distribution with 2 degrees of freedom.
is the same as the chi-squared
distribution with 2 degrees of freedom.
The above result can be used to simulate (or generate) normal random variables
by making a suitable transformation on uniform random variables by making a
suitable transformation on uniform random variables. Let U1 and U2 be
independent random variables each uniformly distributed over (0,1). We will
transform U1,U2 into two independent coordinate representation
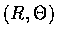 of the random vector (X1,X2). From the above,
of the random vector (X1,X2). From the above,
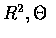 will be
independent, and, in addition,
R2=X12+X22 will have an exponential
distribution with parameter
will be
independent, and, in addition,
R2=X12+X22 will have an exponential
distribution with parameter
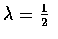 .
But
.
But
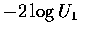 has such a
distribution since, for x>0
has such a
distribution since, for x>0
Also, as 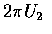 is a uniform
is a uniform 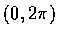 random variable, we can use it to
generate
random variable, we can use it to
generate 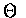 .
That is, if we let
then R2 can be taken to be the square of the distance from the origin and
.
That is, if we let
then R2 can be taken to be the square of the distance from the origin and
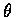 as the angle of orientation of (X1,X2). As
as the angle of orientation of (X1,X2). As
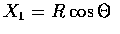 ,
,
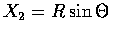 ,
we obtain that
are independent unit normal random variables.
,
we obtain that
are independent unit normal random variables.
![$\rule[0.02em]{1.0mm}{1.5mm}$](img27.gif)
![]() and
and
![]() ,
we see
that
,
we see
that
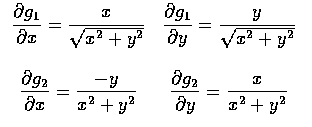
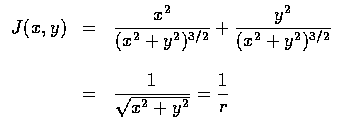
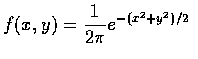
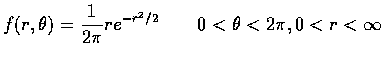
![]() ,
then, as the
transformation
d=g1(x,y)=x2+y2 and
,
then, as the
transformation
d=g1(x,y)=x2+y2 and
![]() has a
Jacobian
has a
Jacobian
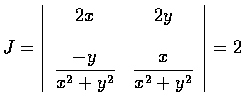
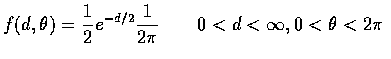
![]() of the random vector (X1,X2). From the above,
of the random vector (X1,X2). From the above,
![]() will be
independent, and, in addition,
R2=X12+X22 will have an exponential
distribution with parameter
will be
independent, and, in addition,
R2=X12+X22 will have an exponential
distribution with parameter
![]() .
But
.
But
![]() has such a
distribution since, for x>0
has such a
distribution since, for x>0