No Title

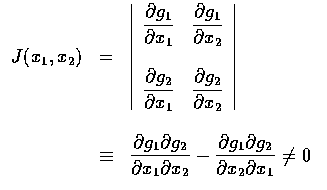
Joint Probability Distribution Functions of Random Variables

設 X₁ 和 X₂ 為聯合連續隨機變數, 其聯合機率密度函數為 f_{x₁ ,x₂}. 有時我們必需去算 Y₁ 和 Y₂ 的聯合分布, 其中 Y₁ 和 Y₂ 分別是 X₁ 和 X₂ 的函數. 特別地, 對某些函數 g₁ 和 g₂, 我們令 Y₁ = g₁ (X₁,X₂),Y₂ = g₂ (X₁,X₂). 假設函數 g₁ 和 g₂ 滿足下列條件:

假設 1.: 方程組 y₁ = g₁ (x₁,x₂) 和 y₂ = g₂ (x₁,x₂) 有唯一解, 設其解為 x₁ = h₁ (y₁,y₂), x₂ = h₂ (y₁, y₂).
假設 2.: 函數 g₁ 和 g₂ 在所有點 (x₁,x₂) 的偏微分都存在且連續; 同時對所有點 (x₁,x₂), 下述 $2 \times 2$ 的行列式
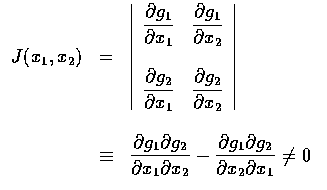
$\begin{array}{rcl} J(x_1,x_2)&=&\left \vert \begin{array}{cc} \displaystyle\fra... ...2}- \frac{\partial g_1\partial g_2}{\partial x_2\partial x_1}\neq 0 \end{array}$

在這兩個條件下, 可以證得 Y₁ 和 Y₂ 為聯合連續隨機變數, 其聯合密度函數為

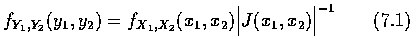
$f_{Y_1,Y_2}(y_1,y_2)=f_{X_1,X_2}(x_1,x_2)\Big \vert J(x_1,x_2)\Big \vert^{-1} \qquad(7.1)$

其中 x₁ = h₁ (y₁,y₂), x₂ = h₂ (y₁,y₂). 其中上式 (7.1) 的證明可依下述步驟進行:

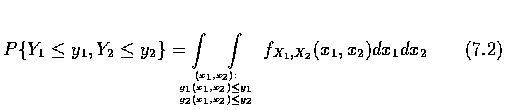
$P\{ Y_1\leq y_1,Y_2\leq y_2\}= \displaystyle\int\int \limits_{{\hspace{-0.7cm}... ...space{-0.7cm}g_2(x_1,x_2 )\leq y_2} f_{X_1,X_2} (x_1,x_2) dx_1 dx_2\qquad (7.2)$

其聯合密度函數可由上式 (7.2) 對 y₁ 和 y₂ 微分得到. 而微分的結果會等於 (7.1) 式之右邊.

Example: If X and Y are independent gamma random variables with parameters $(\alpha ,\lambda)$ and $(\beta ,\lambda)$ , respectively, compute the joint density of U=X+Y and V=X/(X+Y).
Solution:: The joint density of X and Y is given by
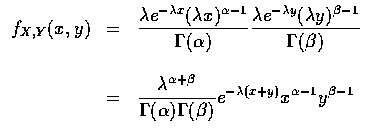
$\begin{array}{rcl} f_{X,Y}(x,y)&=& \displaystyle\frac{\lambda e^{-\lambda x}(\l... ...(\alpha)\Gamma (\beta)} e^{-\lambda (x+y)}x^{\alpha -1}y^{\beta -1} \end{array}$
Now, if g₁(x,y)=x+y, g₂(x,y)=x/(x+y), then
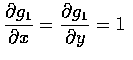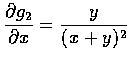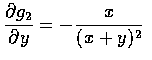
$\displaystyle\frac{\partial g_1}{\partial x}=\frac{\partial g_1}{\partial y}=1$ , $\displaystyle\frac{\partial g_2}{\partial x}=\frac{y}{(x+y)^2}$ , $\displaystyle\frac{\partial g_2}{\partial y}=-\frac{x}{(x+y)^2}$
and so
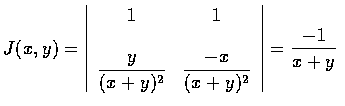
$J(x,y)=\left \vert \begin{array}{cc} 1&1 \\ \\ \displaystyle\frac{y}{(x+y)^2}&... ...laystyle\frac{-x}{(x+y)^2} \end{array}\right \vert =\displaystyle\frac{-1}{x+y}$
Finally, as the equations u=x+y,v=x/(x+y) have as their solutions x=uv,y=u(1-v), we see that
$\begin{array}{rcl} f_{U,V}(u,v)&=&f_{X,Y}[uv, u(1-v)]u \\ \\ &=&\displaystyle\... ...}(1-v)^{\beta-1}\Gamma(\alpha+\beta)} {\Gamma(\alpha)\Gamma(\beta)} \end{array}$
Hence X+Y and X/(X+Y) are independent, with X+Y having a gamma distribution with parameters $(\alpha+\beta,\lambda)$ and X/(X+Y) having a beta distribution with parameters $(\alpha,\beta)$ . The above also shows that $B(\alpha,\beta)$ , the normalizing factor in the beta density, is such that
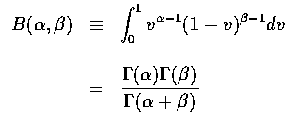
$\begin{array}{rcl} B(\alpha,\beta)&\equiv&\displaystyle\int_0^1v^{\alpha-1}(1-v... ...isplaystyle\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)} \end{array}$

The above result is quite interesting. For suppose there are n+m jobs to be performed, with each (independently) taking an exponential amount of time with rate $\lambda$ for performance, and suppose that we have two workers to perform these jobs. Worker A will do jobs $1,2,\ldots ,n$ , and worker B will do the remaining m jobs. If we let X and Y denote the total working times of workers A and B, respectively, then X and Y will be independent gamma random variables having parameters $(n,\lambda)$ and $(m,\lambda)$ , respectively. Then the above result yields that independently of the working time needed to complete all n+m jobs (that is, of X+Y), the proportion of this work that will be performed by worker A has a beta distribution with parameters $(n,m)\qquad\rule[0.02em]{1.0mm}{1.5mm}$