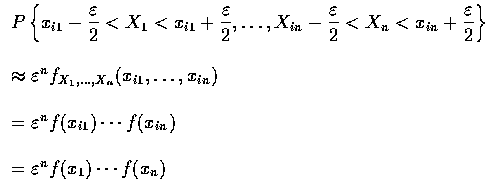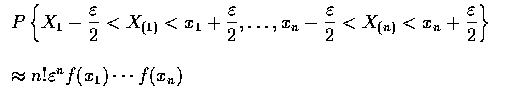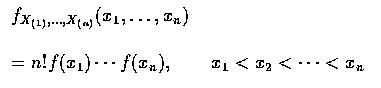Order Statistics
設
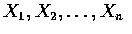 為 n 個獨立且具有相同分布的連續隨機變數,
其共同的密度函數為 f, 共同的密度函數為 F.
為 n 個獨立且具有相同分布的連續隨機變數,
其共同的密度函數為 f, 共同的密度函數為 F.
Definition
則有序變數
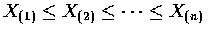 稱為對應於隨機變數
稱為對應於隨機變數
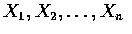 的 順序統計量 (order statistics). 換句話說,
的 順序統計量 (order statistics). 換句話說,
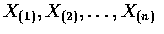 為
為
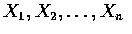 的順序值.
的順序值.
順序統計量的聯合密度函數可求之如下: 順序統計量
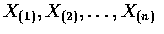 所取的值為
所取的值為
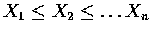 的充要條件為對
的充要條件為對
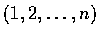 的某一排列
的某一排列
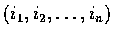 ,
,
因為, 對
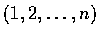 的任一排列
的任一排列
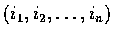 故得, 對
故得, 對
 將上式兩端除以
將上式兩端除以
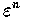 且令
且令
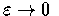 得
上式的最簡單的解釋如下: 為了使向量
得
上式的最簡單的解釋如下: 為了使向量
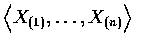 的值為
的值為
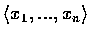 ,
其充分必要條件是
,
其充分必要條件是
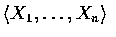 等於
等於
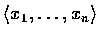 的 n! 種排列中的一種. 又因為
的 n! 種排列中的一種. 又因為
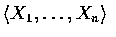 等於
等於
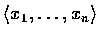 的任一排列的機率密度為
的任一排列的機率密度為
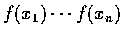 ,
故得上式.
,
故得上式.
![]() 為 n 個獨立且具有相同分布的連續隨機變數,
其共同的密度函數為 f, 共同的密度函數為 F.
為 n 個獨立且具有相同分布的連續隨機變數,
其共同的密度函數為 f, 共同的密度函數為 F.
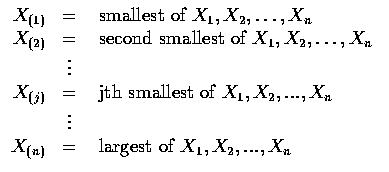
![]() 所取的值為
所取的值為
![]() 的充要條件為對
的充要條件為對
![]() 的某一排列
的某一排列
![]() ,
,