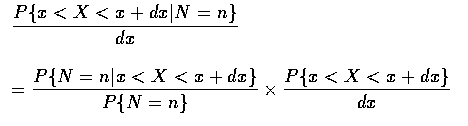
Conditional Distribution - Continuous Case and Discrete Case

當隨機變數不是聯合連續隨機變數也不是聯合離散隨機變數時, 我們也可討論隨機變數的條件分布. 例如, 設 X 為一連續隨機變數, 其機率密度函數為 f, 而 N 為一離散隨機變數, 現在考慮在給予 N=n 的條件下, X 的條件分布函數. 因為

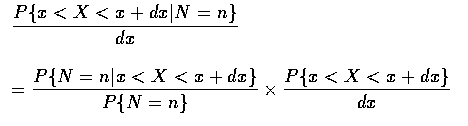
$\begin{array}{l} \displaystyle\frac{ P\{ x < X < x+dx \vert N=n\} } {dx} \\ \\ ... ...< X <x+dx \} }{ P\{N=n\} } \times \frac{ P\{x < X < x+dx \} } {dx} \end{array}$
令 dx 趨近於 0 得
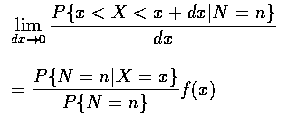
$\begin{array}{l} \displaystyle\lim_{dx \rightarrow 0 } \frac{ P\{x<X<x+dx \vert... ...} \\ \\ =\displaystyle\frac{ P\{N=n\vert X=x \} }{ P\{N=n\} } f(x) \end{array}$
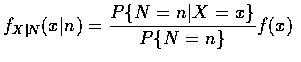
此證明了在給予 N=n 時, X 的條件密度函數為 $f_{X\vert N} (x\vert n) = \displaystyle\frac{ P\{N=n\vert X=x\} }{ P\{N=n\} } f(x) $

Example
考慮有相同成功機率的 n+m 次試行. 但假設此成功機率事先並沒有 固定而是選自均勻 (0,1) 母體. 試求在 n+m 次試行中成功 n 次的條件下, 成功機率的條件分布是什麼?
Solution:
令 X 表示試行的成功機率, 則 X 為在區間 (0,1) 上均勻分布的隨機變數. 又在給定 X=x 時, 此 x+m 次試行為互相獨立且有共同的成功機率 x, 所以成功的次數 N 為參數是 (n+m ,x ) 的二項隨機變數. 因此, 給予 N=n, X 的條件密度函數為
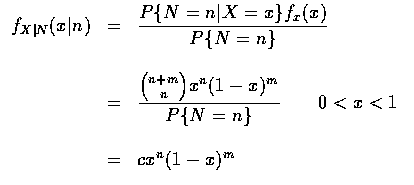
$\begin{array}{rcl} f_{X\vert N} (x\vert n) & = & \displaystyle\frac{ P\{ N=n\ve... ...x^n (1-x)^m } { P\{N=n\} } \qquad 0<x<1 \\ \\ & = & c x^n (1-x)^m \end{array}$
其中 c 與 x 無關. 故所求的條件密度函數為 beta 隨機變數之密度函數, 其參數為 $n+1, m+1\qquad\rule[0.02em]{1.0mm}{1.5mm}$.

The above result is quite interesting, for it states that if the original or prior (to the collection of data) distribution of a trial success probability is uniformly distributed over (0,1) [or, equivalently, is beta with parameters (1,1)] then the posterior (or conditional) distribution given a total of n successes in n+m trials is beta with parameters (1+n,1+m). This is valuable, for it enhances our intuition as to what it means to assume that a random variable has a beta distribution.