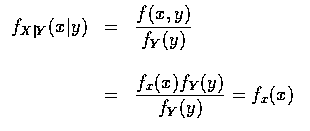Conditional Distribution - Continuous Case

設 X 和 Y 的聯合機率密度函數為 f(x,y), 則對每一滿足 fY (y) > 0的 y 值, 函數

$ f_{X\vert Y} = \displaystyle\frac{f(x,y)}{ f_Y(y) } $
稱為在 Y=y 時, X 的條件機率密度函數. 作這樣定義的動機如下 : 將上式的左邊 乘上 dx, 右邊乘上 (dxdy)/dy 得
$\begin{array}{rcl} f_{X\vert Y} (x\vert y) dx & = & \displaystyle\frac{f(x,y) d... ...} \\ \\ & = & P\{ x \leq X \leq x+dx \vert y \leq Y \leq y+dy \} \end{array} $
也就是說, 對很小的 dx 和 dy 值, fX|Y (x|y) dx 表示在 Y 介於 y和 y+dy 間時, X 介於 x 和 x+dx 間的條件機率.

在給予一隨機變數的值後, 條件密度函數可用來定義與另一隨機變數有關之事件的條件 機率. 也就是說, 若 X 和 Y 為結合連續隨機變數, 則對任意事件 A,

$ P\{ X\in A \vert Y=y \} = \displaystyle\int_A f_{X\vert Y} (x\vert y) dx $
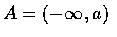特別當 $A=(-\infty, a) $ 時, 我們可定義在 Y=y 時, X 的條件累積分布函數 為
$F_{X\vert Y}(a\vert y)\equiv P\{X\leq a\vert Y=y\}=\displaystyle\int_{-\infty}^a f_{X\vert Y}(x\vert y)dx$
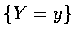利用上面討論所呈現的觀點, 即使在所給事件 (即, 事件 $\{Y=y\}$之機率為 0 的情況下, 我們也能成功的表示條件機率.

Example
設 X 和 Y 的聯合密度函數為
$ f(x,y) = \left \{ \begin{array}{ll} \displaystyle\frac{e^{-x/y} e^{-y} }{y} & ... ...nfty, 0 < y < \infty \\ \\ 0 & \qquad \mbox{ otherwise } \end{array} \right .$
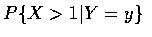求 $ P\{ X>1 \vert Y=y \} $ .
Solution:
首先我們求在給予 Y=y 時, X 的條件密度函數 C .
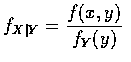
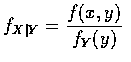
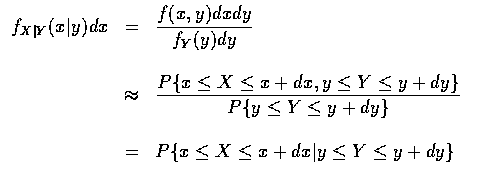
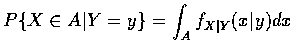
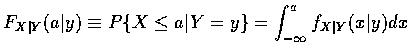
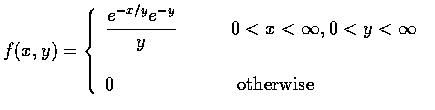
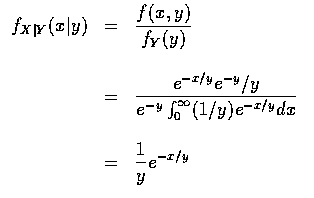
$\begin{array}{rcl} f_{X\vert Y} (x\vert y)&=&\displaystyle\frac{f(x,y) }{ f_Y (... ...nfty (1/y) e^{-x/y} dx }\\ \\ &=&\displaystyle\frac{1}{y} e^{-x/y} \end{array}$
因此,
$\begin{array}{rcl} P\{ X>1 \vert Y=y \} & = & \displaystyle\int_1^\infty \frac{... ...rt _1^\infty \\ \\ & = & e^{-1/y}\qquad\rule[0.02em]{1.0mm}{1.5mm} \end{array}$

若 X 和 Y 為獨立的連續隨機變數, 則給予 Y=y, X 的條件密度函數正好是 X 的無條件密度函數. 這是因為在獨立的假設下, 我們有

$\begin{array}{rcl} f_{X\vert Y}(x\vert y)&=&\displaystyle\frac{f(x,y)}{f_Y(y) } \\ \\ &=&\displaystyle\frac{f_x(x) f_Y (y) } { f_Y (y) } = f_x (x) \end{array}$
的緣故.