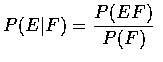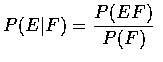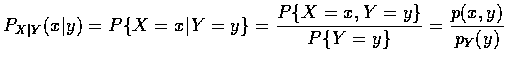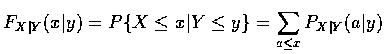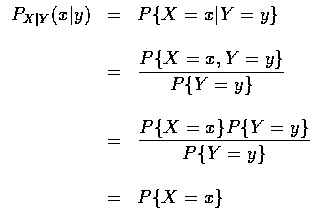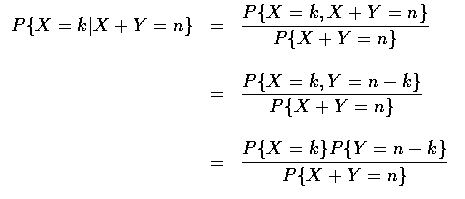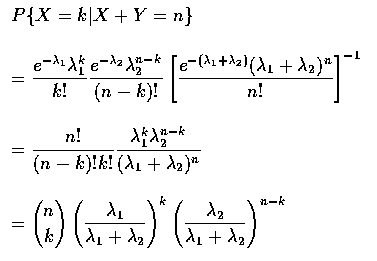Conditional Distributions - Discrete Case

對任意兩事件 E 和 F, 若 P(F) > 0, 則在給予 F 後, 事件 E之條件機率的定義為

$ P(E\vert F) = \displaystyle\frac{P(EF)}{P(F)} $
因此, 當 X 和 Y 為離散隨機變數時, 很自然的對所有滿足 pY (y) > 0 的 y, 定義在給予 Y = y 的條件下, X 的 條件機率質量函數 (conditional probability mass function) 為
$ P_{X\vert Y} (x\vert y) = P\{X=x \vert Y=y \} = \displaystyle\frac{P\{X=x, Y=y\} }{ P\{Y=y\} } = \frac{p(x,y) }{p_Y(y)}$
同樣, 對所有滿足 pY (y) > 0 的 y, 定義在給予 Y=y 的條件下, X 的 條件機率分布函數 (conditional probability distribution function) 為
$F_{X\vert Y}(x\vert y)=P\{ X\leq x\vert Y\leq y\} =\displaystyle\sum_{a \leq x} P_{X\vert Y} (a\vert y) $
換句話說, 上述的定義方式和無條件的情況是完全一樣的, 只是現在的每一件事都要以 事件 Y=y 作為條件. 若 X 獨立於 Y, 則條件質量函數與條件分布函數和無條件 的情形是一樣的. 這是因為當 X 獨立於 Y 時, 我們有
$\begin{array}{rcl} P_{X\vert Y} (x\vert y) & = & P\{ X=x \vert Y=y \} \\ \\ & ... ...splaystyle\frac{P\{X=x\}P\{Y=y\} }{P\{Y=y\} } \\ \\ & = & P\{X=x\} \end{array}$
的緣故.

Example
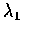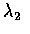設 X 和 Y 為獨立卜瓦松隨機變數, 其參數分別是 $\lambda _1 $ 和 $ \lambda _2 $, 若已知 X+Y = n, 求 X 的條件分布.
Solution:
我們求在給予 X+Y=n 的條件下, X 的條件機率質量函數如下:
$\begin{array}{rcl} P\{X=k \vert X+Y=n \} & = & \displaystyle\frac{P\{X=k, X+Y =... ...\\ & = & \displaystyle\frac{P \{ X=k\} P\{Y=n-k\} }{ P\{X+Y=n\} } \end{array}$
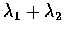其中最後一個等式是根據獨立性的假設得到的. 而 X + Y 為參數是 $ \lambda _1 + \lambda _2 $ 的卜瓦松隨機變數. 所以上式等於
$\begin{array}{l} P\{X=k\vert X+Y=n\} \\ \\ = \displaystyle\frac{e^{-\lambda _1... ...k \left ( \frac{\lambda _2}{\lambda _1 + \lambda _2} \right )^{n-k} \end{array}$
換句話說, 給予 X+Y=n, X 的條件分布為二項分布, 其參數為 n 和 $ \lambda /(\lambda _1 + \lambda _2 ) \qquad\rule[0.02em]{1.0mm}{1.5mm}$.