No Title

Chi-Squared Distribution

Example: Let $X_1,X_2,\ldots ,X_n$ be n independent exponential random variables each having parameter $\lambda$ . Then, as an exponential random variable with parameter $\lambda$ is the same as a gamma random variable with parameters $(1,\lambda)$ , and that $X_1+X_2+\cdots +X_n$ is a gamma random variable with parameters $(n,\lambda)\qquad \rule[0.02em]{1.0mm}{1.5mm}$

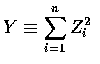If $Z_1,Z_2,\ldots Z_n$ are independent unit normal random variables, then $Y\equiv\displaystyle\sum_{i=1}^n Z_i^2$ is said to have the chi-squared (sometimes seen as $\chi^2$ ) distribution with n degrees of freedom. Let us compute its density function. When n=1, Y=Z₁², and that its probability density function is given by

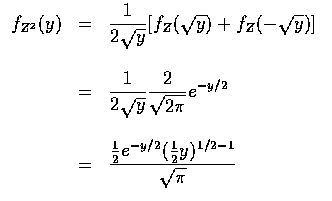
$\begin{array}{rcl} f_{Z^2}(y)&=&\displaystyle\frac{1}{2\sqrt{y}}[f_Z(\sqrt{y})+... ...aystyle\frac{\frac{1}{2}e^{-y/2}(\frac{1}{2}y)^{1/2-1}}{\sqrt{\pi}} \end{array}$

But we recognize the above as the gamma distribution with parameters $(\frac{1}{2},\frac{1}{2})$ . [A by-product of this analysis is that $\Gamma (\frac{1}{2})=\sqrt{n}$ .] But as each Z_i² is gamma $(\frac{1}{2},\frac{1}{2})$ . That the $\chi^2$ distribution with n degrees of freedom is just the gamma distribution with parameters $[n/2,\frac{1}{2}]$ and hence has a probability density function given by

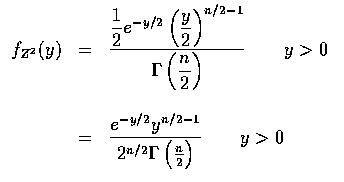
$\begin{array}{rcl} f_{Z^2}(y)&=&\displaystyle \frac{\displaystyle\frac{1}{2}e^{... ...y/2}y^{n/2-1}} {2^{n/2}\Gamma\left (\frac{n}{2}\right )} \qquad y>0 \end{array}$

When n is an even integer, $\Gamma (n/2)=[(n/2)-1]!$ , whereas when n is odd, $\Gamma (n/2)$ can be obtained from iterating the relationship $\Gamma (\frac{1}{2})=\sqrt{n}$ . [For instance, $\Gamma (\frac{5}{2})=\frac{3}{2}\Gamma (\frac{3}{2})= \frac{3}{2}\frac{1}{2}\Gamma (\frac{1}{2})=\frac{3}{4}\sqrt{\pi}$

The chi-sqarted distribution often arises in practice as being the distribution of the square of the error involved when one attempts to hit a target in n-dimensional space when the coordinate errors are taken to be independent until normal random variables. It is also important in statistical analysis.