Sums of Independent Random Variables

當 X 和 Y 為獨立隨機變數時, 一件重要的事是要能夠從 X 和 Y 的分布函數, 求得 X+Y 的分布函數. 假設 X 和 Y 為獨立連續隨機變數, 其機率密度函數分別為 fX 和 fY. 則 X+Y 的分布函數可求之如下:

$\begin{array}{rcl} F_{X+Y} (a) & = & P \{ X+Y \leq a \} \\ \\ &=& \displaystyl... ...style\int_{-\infty}^\infty F_x (a-y) f_Y (y) dy \qquad \qquad (3.1) \end{array}$
累積分布函數 FX+Y 稱為分布函數 FX 和 FY 的 褶積 (convolution) (FX 和 FY 分別是 X 和 Y 的累積分布函數).

將 (3.1) 式微分得 X+Y 的機率密度函數 fX+Y 如下:

$\begin{array}{rcl} f_{X+Y}(a)&=&\displaystyle\frac{d}{da} \int_{-\infty}^\infty... ...displaystyle\int_{-\infty}^\infty f_X (a-y) f_Y (y) dy \qquad (3.2) \end{array}$

Example (Sum of Two Independent Uniform Random Variables
兩個獨立的均勻隨機變數的和. 設 X 和 Y 為獨立隨機變數, 且兩個均在 (0,1) 上均勻分布, 求 X+Y 的機率密度函數.
Solution:
因
$f_X (a) = f_Y (a) = \left \{ \begin{array}{ll} 1 & \qquad 0<a<1 \\ 0 & \qquad \mbox{ otherwise } \end{array}\right. $
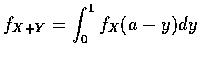
故由上面 (3.2) 可得 $ f_{X+Y} = \displaystyle\int_0^1 f_X (a-y) dy $
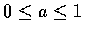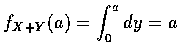
當 $0 \leq a \leq 1 $ 時, 得 $ \displaystyle f_{X+Y} (a) = \displaystyle\int_0^a dy=a $
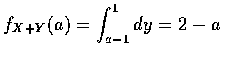
當 1<a<2 時, 得 $ \displaystyle f_{X+Y} (a) = \int_{a-1}^1 dy = 2-a $
所以
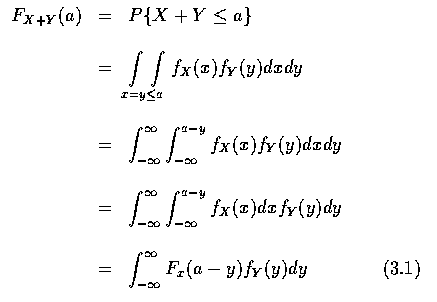
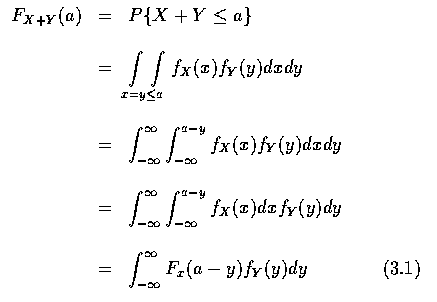
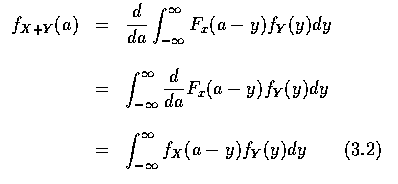
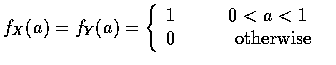
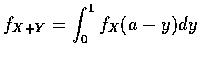
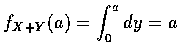
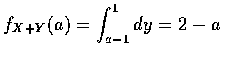
$f_{X+Y} (a) = \displaystyle\left \{ \begin{array}{ll} a & \qquad 0 \leq a \leq... ...quad \mbox{ otherwise } \qquad \rule[0.02em]{1.0mm}{1.5mm} \end{array}\right . $