No Title

Independent of n random variables

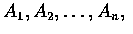
當然, 獨立的概念也可適用於兩個以上的隨機變數. 一般而言, 若對所有的實數集合 $A_1, A_2,\ldots , A_n,$

$P\{ X_1\in A_1,X_2\in A_2,\ldots ,X_n\in A_n\} = \displaystyle\Pi\limits_{i=1}^nP\{X_i\in A_i\}$

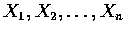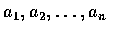則稱此 n 個隨機變數 $X_1, X_2,\ldots ,X_n$ 為獨立隨機變數. 與前面一樣, 可證得此條件相當於 : 對所有的實數 $a_1, a_2,\ldots , a_n$ ,

$P\{ X_1\leq a_1,X_2\leq a_2,\ldots ,X_n\leq a_n\} = \displaystyle\Pi\limits_{n=1}^nP\{ X_i\leq a_i\}$

最後, 對一無窮序列的隨機變數而言, 若它的任意有限子集合均為獨立的話, 則稱此無窮序列的隨機變數為獨立.

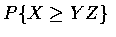Example: Let X,Y,Z be independent and uniformly distributed over (0,1). Compute $P\{X\geq YZ\}$ .
Solution:: Since
f_X,Y,Z(x,y,z)=f_X(x)f_Y(y)f_Z(z)=1
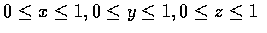
$0\leq x\leq 1, 0\leq y\leq 1, 0\leq z\leq 1$
we have
$\begin{array}{rcl} P\{X\geq YZ\}&=&\displaystyle\int\int\int\limits_{\hspace{-0... ...\ \\ &=&\displaystyle\frac{3}{4} \qquad\rule[0.02em]{1.0mm}{1.5mm} \end{array}$