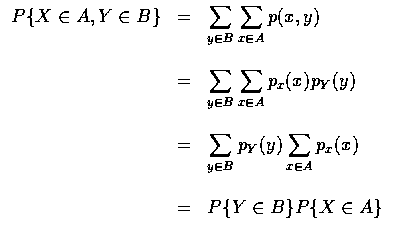Independent Random Variables

若對任意兩個實數集合 A 和 B

$P\{ X \in A, Y \in B \} = P\{X \in A \} P\{ Y \in B \}\qquad (2.1)$
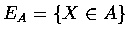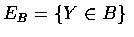則稱隨機變數 X 和 Y 獨立 (independent). 換句話說, 若對所有的 A 和 B, 事件 $E_A = \{ X \in A \} $ 和 $ E_B = \{ Y \in B \} $ 為獨立事件, 則 X 和 Y 為獨立隨機變數.

利用機率的三個 Axiom, 我們可以證得上式成立的充要條件為

$\forall a,b\qquad P\{X\leq a,Y\leq b\}=P\{X\leq a\} P\{Y\leq b \}$
因此, 若使用 X 和 Y 的聯合分布函數 F, 那麼當對所有的 a,b
F(a,b) = FX (a) FY (b)
時, 我們得 X 和 Y 為獨立隨機變數.

當 X 和 Y 為離散隨機變數時, 獨立的條件 (2.1) 相當於對所有的 x 和 y

$ p(x,y) = p_X (x) p_Y (y) \qquad (2.2) $
其等價關係如下: 若 (2.1) 式成立, 則分別令 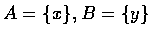$ A = \{x\}, B = \{y\} $, 即可得 (2.2) 式. 又若 (2.2) 式成立, 則對任意 A 和 B
$\begin{array}{rcl} P\{ X \in A, Y \in B \} & = & \displaystyle\sum_{y\in B} \su... ...Y(y) \sum_{x\in A} p_x (x) \\ \\ & = & P\{Y \in B\} P\{X \in A \} \end{array}$
因此得 (2.1) 式 .

在聯合連續的情況下, 獨立的條件相當於對所有的 x 和 y

f(x,y) = fX (x) fY (y)
因此, 大致來說, 對任意二隨機變數 X 和 Y, 若知道其中一個的值不會改變另一個的分布, 則 X 和 Y 為獨立隨機變數. 不是獨立的隨機變數稱之為相依 (dependent).