No Title

Multinomial Distribution

我們可以利用與兩個隨機變數完全同樣的方法來定義 n 個隨機變數的聯合機率分布. 例如, n 個隨機變數 $X_1,X_2,\ldots ,X_n$ 的聯合累積機率分布函數 $F(a_1,a_2,\ldots ,a_n)$ 的定義為

$F(a_1,a_2,\ldots ,a_n)=P\{X_1\leq a,X_2\leq a_2,\ldots ,X_n\leq a_n\}$

又若存在一個函數 $f(x_1,x_2,\ldots ,x_n)\geq 0$ 對 n 維空間中任一集合 C,

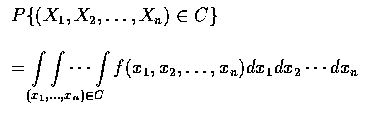
$\begin{array}{l} P\{(X_1,X_2,\ldots ,X_n)\in C\} \\ \\ =\displaystyle\int\int\... ...}(x_1,\ldots ,x_n)\in C} f(x_1,x_2,\ldots ,x_n)dx_1dx_2\cdots dx_n \end{array}$

則稱此 n 個隨機變數為聯合連續隨機變數; 而 $f(x_1,x_2,\ldots ,x_n)$ 則稱為它們的聯合機率密度函數. 特別當 $A_1,A_2,\ldots ,A_n$ 為 n 個實數集合時,

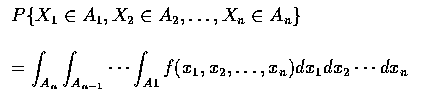
$\begin{array}{l} P\{X_1\in A_1,X_2\in A_2,\ldots ,X_n\in A_n\} \\ \\ =\display... ...{A_{n-1}}\cdots\int_{A1} f(x_1,x_2,\ldots ,x_n) dx_1dx_2\cdots dx_n \end{array}$

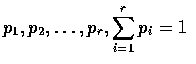Example (The Multinomial Distribution): One of the most important joint distributions is the multinomial, which arises when a sequence of n independent and identical experiments is performed. Suppose that each experiment can result in any one of r possible outcomes, with respective probabilities $p_1, p_2,\ldots ,p_r,\displaystyle\sum_{i=1}^r p_i=1$ . If we denote by X_i, the number of the n experiments that result in outcome number i, then
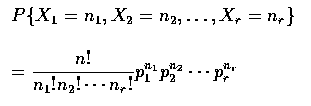
$\begin{array}{l} P\{X_1=n_1,X_2=n_2,\ldots ,X_r=n_r\} \\ \\ =\displaystyle\frac{n!}{n_1!n_2!\cdots n_r!}p_1^{n_1}p_2^{n_2}\cdots p_r^{n_r} \end{array}$
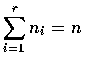whenever $\displaystyle\sum_{i=1}^{r}n_i=n$ .
UP equation is verified by noting that any sequence of outcomes for the nexperiments that leads to outcome i occurring n_i times for $i=1,2,\ldots ,r$ will, by the assumed independence of experiments, have probability $p_1^{n_1}p_2^{n_2}\cdots p_r^{n_r}$ of occurring. As there are $n!/(n_1!n_2!\cdots n_r!)$ such sequences of outcomes (there are $n!/(n_1!n_2!\cdots n_r!)$ different permutations of n things of which n₁are alike, n₂ are alike, ... , n_r are alike), up equation is established. The joint distribution whose joint probability mass function is specified of up, is called the multinomial distribution. When r=2, the multinomial readuces to the binomial distribution. $\rule[0.02em]{1.0mm}{1.5mm}$