Example
- Example
- The joint density function of X and Y is given by
Compute (a)
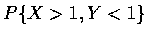 ,(b)
,(b) 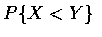 ,
and (c) P{X<a}.
,
and (c) P{X<a}.
- Solutions:
- (a)
(b)
(c)
- Example
- The joint density of X and Y is given by
Find the density function of the random variable X/Y.
- Solutions:
- We start by computing the distribution function of X/Y. For a>0,
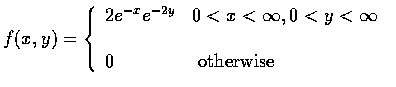
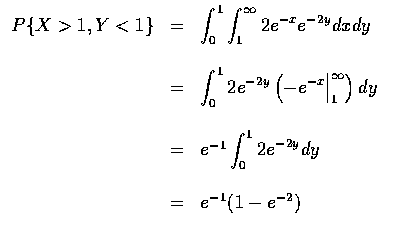
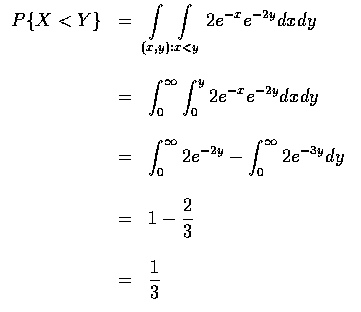
![$\begin{array}{rcl}
P\{X<a\}&=&\displaystyle\int_0^a\int_0^\infty 2e^{-2y}e^{-x}...
...t_0^a e^{-x}dx \\ \\
&=&1-e^{-a} \qquad\rule[0.02em]{1.0mm}{1.5mm}
\end{array}$](img6.gif)
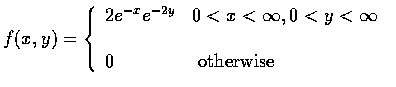
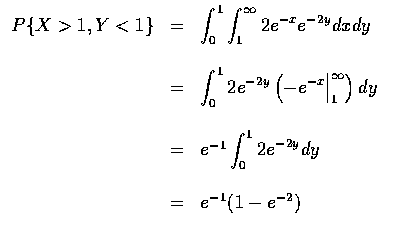
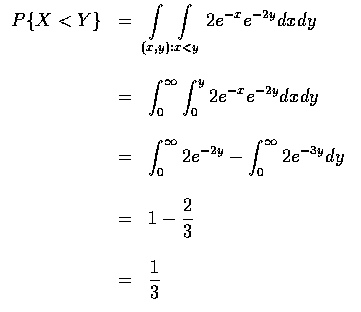
![$\begin{array}{rcl}
P\{X<a\}&=&\displaystyle\int_0^a\int_0^\infty 2e^{-2y}e^{-x}...
...t_0^a e^{-x}dx \\ \\
&=&1-e^{-a} \qquad\rule[0.02em]{1.0mm}{1.5mm}
\end{array}$](img6.gif)

![$\begin{array}{rcl}
F_{X/Y}(a)&=&P\left\{\displaystyle\frac{X}{Y}\leq a\right\} ...
...\right ]\Big \vert _0^\infty \\ \\
&=&1-\displaystyle\frac{1}{a+1}
\end{array}$](img9.gif)