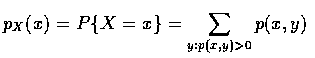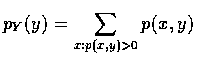No Title

Joint Cumulative Probability Distribution Functions

到目前為止, 我們只討論了一個隨機變數的機率分布. 然而我們卻經常對兩個或更多隨機變數的機率敘述感到興趣. 為了討論這一類的機率問題, 對任意的兩個隨機變數 X 和 Y, 我們定義 X 和 Y 的 聯合累積機率分布函數 (joint cunulative probability distribution function) 為

$F(a,b) = P\{ X \leq a, Y \leq b \} \qquad -\infty < a,b < \infty$

X 的分布可從 X 和 Y 的聯合分布得之如下:

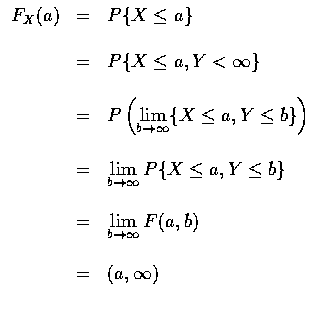
$\begin{array}{rcl} F_X(a) & = & P\{X \leq a \} \\ \\ & = & P\{ X\leq a, Y < \i... ...lim_{b \rightarrow \infty } F(a,b) \\ \\ & = & (a, \infty) \\ \\ \end{array}$

注意在上面的一些等式中, 我們一再地使用機率是連續集合(即事件) 函數的性質. 同理可得 Y 的累積分布函數為

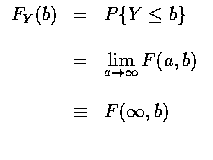
$\begin{array}{rcl} F_Y(b) & = & P \{ Y \leq b \} \\ \\ & = & \displaystyle\lim_{a \rightarrow \infty } F(a,b) \\ \\ & \equiv & F(\infty, b ) \\ \\ \end{array}$

分布函數 F_X 和 F_Y 有時稱之為 X 和 Y 的 邊際分布 (marginal distribution).

所有有關 X 和 Y 的聯合機率敘述, 理論上都可由它們的聯合分布函數得到. 例如, 欲求 X 大於 a 且 Y 大於 b 的機率, 則可求之如下:

$\begin{array}{rcl} P\{ X > a, Y > b \} & = & 1 - P (\{ X>a, Y>b \}^c) \\ \\ & ... ..., Y \leq b \} ] \\ \\ & = & 1 - F_X (a) - F_Y (b) + F(a,b) \\ \\ \end{array}$

上式事實上可以視為下式的一個特例,

$P\{a_1<X\leq\a_2, b_1<Y\leq b-2\}=F(a_2,b_2)+F(a_1,b_1)-F(a_1,b_2)-F(a_2,b_1)$

whenever a₁<a₂, b₁<b₂.

當 X 和 Y 同為離散隨機變數時, 我們定義 X 和 Y 的 聯合機率質量函數(joint probability mass function ) 如下:

$P(x,y) = P \{X =x, Y=y \}$

X 的機率質量函數可由 p(x,y) 求得如下:

$p_X (x) = P\{ X =x \} = \displaystyle\sum_{y:p(x,y)>0} p(x,y)$

同理可得

$p_Y (y) = \displaystyle\sum_{x:p(x,y)>0 } p(x,y)$