The Distribution of a Function of a Random Variable
通常的情況是我們知道一隨機變數的機率分布,
而我們有興趣的是要決定它的某些函數的分布. 例如, 假設我們知道 X 的分布,
而要求 g(X) 的分布. 欲得此結果, 必需以 X 在某一集合中的形式來表示事件
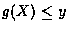 .
我們以下面的例子來說明.
.
我們以下面的例子來說明.
- Example
- 設 X 在區間 (0,1) 上均分分布. 令 Y = Xn, 則 Y 的分布
函數可求之如下: 對
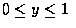 ,
因此, Y 的密度函數為
,
因此, Y 的密度函數為
- Example
- 設 X 為一連續隨機變數, 其機率密度函數為 fx, 則 Y= X2的分布函數可求之如下 : 對
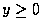 微分得
微分得
- Example
- 設 X 的機率密度函數為 fx, 則 Y = |X| 的密度函數可得之如下:
對
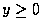 ,
因此, 微分得
,
因此, 微分得
Theorem
設 X 為一連續隨機變數, 其機率密度函數為 fx.
設 g(x) 是 x 的嚴格單調 (遞增或遞減) 可微分 (因而連續) 函數.
則隨機變數 Y = g(X) 有如下的機率密度函數:
其中
g-1 (y) 定義為滿足 g(x) = y 的 x 值.
- Example
- Let X be a continuous nonegative random variable with density function f,
and let Y=Xn. Find fY, the probability density function of Y.
- Solution:
- If g(x)=xn, then
g-1(y)=y1/n and
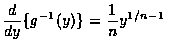 .
.
Hence, from up Theorem, we obtain that
If n=1 this gives
![$f_Y(y)=\displaystyle\frac{1}{\displaystyle2\sqrt{y}}f(\sqrt{y})\qquad\rule[0.02em]{1.0mm}{1.5mm}$](img14.gif)
![]() .
我們以下面的例子來說明.
.
我們以下面的例子來說明.
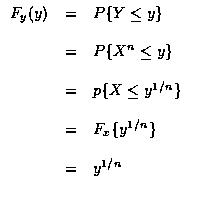
![$ f_y (y) = \left \{ \begin{array}{ll}
\displaystyle\frac{1}{n} y^{1/n-1} & \qq...
... \qquad \mbox{otherwise} \qquad\rule[0.02em]{1.0mm}{1.5mm}
\end{array} \right .$](img4.gif)
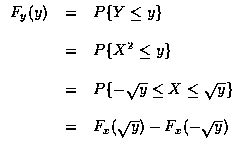
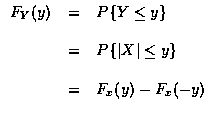
![$ f_Y (y) = \left \{ \begin{array}{ll}
f_x [ g^{-1} (y) ] \Big \vert \displayst...
...x\\ \\
0 & \qquad \mbox{ if } y\neq g(x) \mbox{ for all }
\end{array} \right .$](img11.gif)
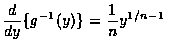 .
.