Other Continuous Distributions

The Weibull Distribution
The weibull distribution function has the form
$F(x)=\left\{\begin{array}{ll} 0&x\leq v \\ \\ 1-\exp\left\{-\left (\displaystyle\frac{x-v}{\alpha}\right )^\beta\right\}&x>v \end{array}\right .$
A random variable whose cumulative distribution function is given by up is said to be a Weifull random variable with parameters $v,\alpha,\beta$. Differentiation yields that the density is
$f(x)\left\{ \begin{array}{ll} 0&x\leq v \\ \\ \displaystyle\left (\frac{\beta}... ...aystyle\frac{x-v}{\alpha}\right )^\beta \right\}&x>v \\ \\ \end{array}\right .$


The Cauchy Distribution
A random variable is said to have a Cauchy distribution with parameter $\theta,-\infty<\theta<\infty$, if its density is given by
$\displaystyle f(x)=\frac{1}{\pi}\frac{1}{[1+(x-\theta)^2]}\qquad -\infty<x<\infty$


The Beta Distribution
A random variable is said to have a beta distribution if its density is given by
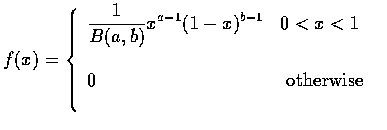
$f(x)=\left\{ \begin{array}{ll} \displaystyle\frac{1}{B(a,b)}x^{a-1}(1-x)^{b-1}&0<x<1 \\ \\ 0&\mbox{ otherwise } \\ \\ \end{array}\right .$
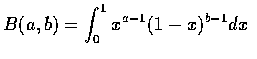
where $B(a,b)=\displaystyle\int_0^1 x^{a-1}(1-x)^{b-1}dx$

The beta distribution can be used to model a random phenomenon whose set of possible values is some finite interval [c,d] -- which by letting c denote the origin and taking d-c as a unit measurement can be transformed into the interval [0,1].

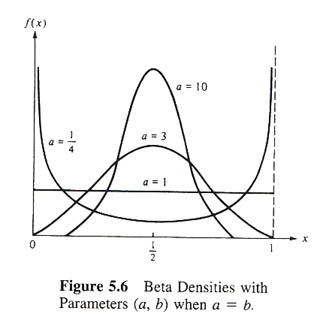
When a=b, the beta density is symmetric about $\displaystyle\frac{1}{2}$, giving more and more weight to regions about $\displaystyle\frac{1}{2}$ as the common value aincreases. (see as follow).

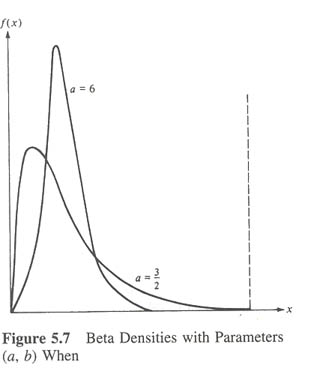
When b>a, the density is skewed to the left (in the sense that smaller values become more likely); and it is skewed to the right when a>b (see as follow).

The following relationship can be shown to exist between

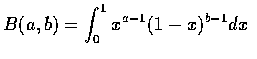
$B(a,b)=\displaystyle\int_0^1 x^{a-1}(1-x)^{b-1}dx$
and the gamma function:
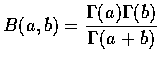
$\displaystyle B(a,b)=\frac{\Gamma (a)\Gamma (b)}{\Gamma (a+b)}$
It is easy matter to show that if X is a beta random variable with parameters a and b, then
$\begin{array}{rcl} E[X]&=&\displaystyle\frac{a}{a+b} \\ \\ Var(X)&=&\displaystyle\frac{ab}{(a+b)^2(a+b+1)} \\ \\ \end{array}$