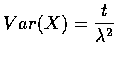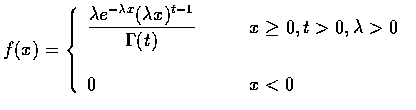
The Gamma Distribution

若一隨機變數的機率密度函數為

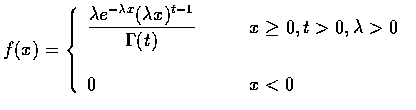
$ f(x) = \left \{ \begin{array}{ll} \displaystyle\frac{\lambda e^{-\lambda x} (... ... \qquad x \geq 0, t>0, \lambda > 0 \\ \\ 0 & \qquad x < 0 \end{array} \right .$
則稱它為參數是 $(t,\lambda )$ 的伽馬隨機變數 (gamma random variable), 其機率分布稱為伽馬分布 (gamma distribution); 其中 $ \Gamma (t) $ 稱為伽馬函數, 其定義為
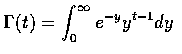
$ \Gamma (t) = \displaystyle\int_0^\infty e^{-y} y^{t-1} dy $
利用部分積分得
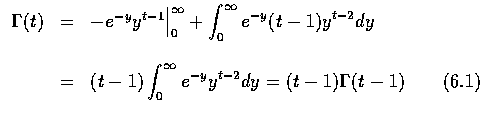
$\begin{array}{rcl} \Gamma (t)&=&-e^{-y} y^{t-1} \Big \vert _0^\infty + \display... ...e\int_0^\infty e^{-y} y^{t-2}dy=(t-1)\Gamma (t-1)\qquad (6.1)\\ \\ \end{array}$
對整數值之 t, 譬如說 t=n, 重複使用上式得
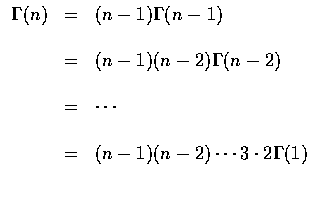
$\begin{array}{rcl} \Gamma (n) & = & (n-1) \Gamma (n-1) \\ \\ & = & (n-1)(n-2)... ...= & \cdots \\ \\ & = & (n-1)(n-2)\cdots 3\cdot 2 \Gamma (1) \\ \\ \end{array}$
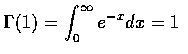因 $\Gamma (1) = \displaystyle\int_0^\infty e^{-x} dx = 1 $, 故得對整數 n, $\Gamma (n) = (n-1)!$

當 t=n 為一正整數時, 具有參數 $(t,\lambda )$ 的伽馬分布在應用上通常是等到 n 個事件發生所需之時間量的分布. 更明確的說, 若事件發生所需的時間是隨機的且滿足第四章第 8 節中的 3 個公設, 則等到 n 個事件發生所需的時間量為參數是 $(n,\lambda )$ 的伽馬隨機變數.

令 Tn 表示第 n 個事件發生的時間, 且注意到 Tn 小於或等於 t 的 充要條件為到時間 t 時所發生的事件數至少為 n, 也就是說, 若以 N(t) 表示 在時間區間 [0,t] 內發生的事件數, 則

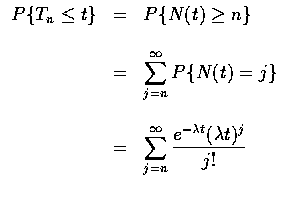
$\begin{array}{rcl} P\{T_n \leq t \} & = & P\{ N(t) \geq n \} \\ \\ & = & \disp... ...\sum_{j=n}^\infty \frac{e^{-\lambda t} (\lambda t)^j } {j!} \\ \\ \end{array} $
其中最後一個等式是因為在 [0,t] 間事件發生的個數為參數是 $\lambda $ 的卜瓦松 分布的緣故. 將上式微分得 Tn 的密度函數如下:
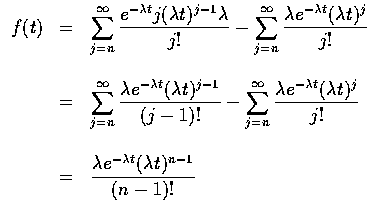
$\begin{array}{rcl} f(t)&=&\displaystyle\sum_{j=n}^\infty \frac{e^{-\lambda t} j... ...laystyle\frac{\lambda e^{-\lambda t} (\lambda t)^{n-1} } { (n-1)! } \end{array}$
因此 Tn 具有參數是 $(n,\lambda )$ 的伽馬分布.

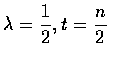$\lambda = \displaystyle\frac{1}{2}, t = \frac{n}{2}$ ( n 為正整數 ) 的伽馬分布稱為 自由度 (degress of freedom) 是 n 的 卡方分布 (chi-squared distribution 或 Xn2 distribution).

Example
設 X 為參數是 $(t,\lambda )$的伽馬隨機變數. 試求 (a) E[X], 和 (b) Var(X).
Solution:
(a)
$\begin{array}{rcl} E[X] & = & \displaystyle\frac{1}{\Gamma (t) } \int_0^\infty ... ...a \Gamma (t) } \\ \\ & = & \displaystyle\frac{t}{\lambda } \\ \\ \end{array} $
(b)
首先求 E[X2], 可得到 $ Var(X) = \displaystyle\frac{t}{\lambda ^2} $