Hazard Rate Functions

考慮一個表示某物品壽命之正值連續隨機變數 X, 設其分布函數為 F, 密度函數為 f. F 的故障率 (hazard rate), 有時稱為失效率 (failure rate) 函數 $\lambda (t)$ 定義為

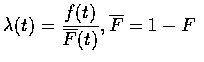
$ \lambda (t) = \displaystyle\frac{f(t)}{\overline{F}(t) }, \overline{F} = 1 - F $
欲說明 $\lambda (t)$, 首先假設該物品已使用了 t 小時, 而我們欲求它將不能再使用另外的 dt 時間的機率. 也就是說, 考慮 $P\{X \in (t,t+dt) \Big \vert X>t\}$. 因
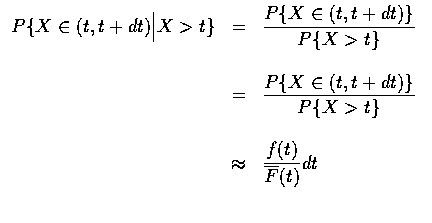
$\begin{array}{rcl} P\{X\in(t,t+dt) \Big \vert X>t\}&=&\displaystyle\frac{P\{X\i... ... \\ \\ &\approx&\displaystyle\frac{f(t)}{\overline{F}(t)}dt \\ \\ \end{array}$
故 $\lambda (t)$ 表示一個已使用 t 單位時間的舊物品即將故障的條件機率密度函數.

現假設壽命分布為指數分布,則由無記憶性可得一個 t 年舊的物其殘餘壽命的分布和 一個新物品的壽命分布是相同的. 因此 $\lambda (t)$ 為一常數. 此可由下面的驗證 得知,

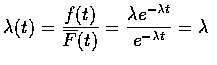
$ \lambda (t) = \displaystyle\frac{f(t)}{\overline{F}(t) } = \frac{\lambda e^{-\lambda t} }{e^{-\lambda t} } = \lambda $
故指數分布的機率函數為一常數. 參數 $\lambda $ 通常稱為分布的率 (the rate of the distribution )

本節最後的結論是故障函數 $\lambda (t)$ 唯一決定分布函數 F. 欲證此結果, 首先根據定義知

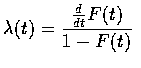
$ \lambda (t) = \displaystyle\frac{ \frac{d}{dt} F(t) }{1- F(t) } $
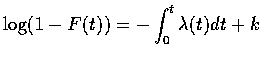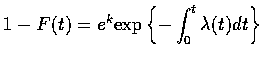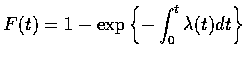
將上式兩邊積分得 $\log (1-F(t)) = - \displaystyle\int_0^t \lambda (t)dt + k$即 $1- F(t) = e^k \mbox{exp} \left \{- \displaystyle\int_0^t \lambda (t) dt \right \}$令 t=0 可證得 k=0, 故得 $F(t) = 1 - \mbox{exp} \left \{ - \displaystyle\int_0^t \lambda (t) dt \right \}$

因此一個正值連續隨機變數的分布函數可由給予它的故障率函數而決定之. 例如, 當一隨機變數有線性故障率函數時, 即 $\lambda (t) = a + bt $則它的分布函數為 F(t) = 1 - e-at-bt2 /2 將上式微分得其密度函數為 $f(t) = (a+bt)e^{-(at+bt^2/2)} \quad, \qquad t \geq 0$當 a=0, 上式稱為 Rayleigh 密度函數.

Example
我們常聽說不論在哪一年齡, 抽煙者的死亡機率為不抽煙者的兩倍. 這句話的意思是什麼呢? 它的意思是指不抽煙者能活過所給之年數的機率為同年齡之抽煙者的兩倍嗎?
Solution:
若 $\lambda _s (t)$ 表示 t 歲吸煙者的故障率, 而 $\lambda _n(t) $ 表示 t 歲不吸煙者的故障率, 則上面的敘述相當於 $ \lambda _s (t) = 2 \lambda _n (t) $一位 A 歲不吸煙者將會活到 B 歲 (A < B) 的機率為

$\begin{array}{rcl} &&P \{ \mbox {A 歲的不吸煙者活到 B 歲} \} \\ \\ &=&P\{\mbox... ...laystyle\exp \left \{ - \int_A^B \lambda _n (t) dt \right \} \\ \\ \end{array}$

同理可得抽煙者的對應機率為

$\begin{array}{rcl} &&P\{ \mbox{A 歲的吸煙者活到 B 歲} \} \\ \\ &=&\exp \left \... ...ft\{-\displaystyle\int_A^B \lambda _n(t) dt \right \} \right ]^2\\ \end{array}$

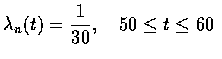換句話說, 在一人抽煙而另一人不抽煙的兩位同年齡的人中, 抽煙者活過任何所給之年紀的機率為不抽煙者之對應機率的平方 (而非一半). 舉例來說, 若 $\lambda _n(t) = \displaystyle\frac{1}{30}, \quad 50 \leq t \leq 60$, 則一位 50 歲的不吸取者活到 60 歲的機率為 $e^{-1/3}\approx 0.7165$, 而非抽煙者的對應機率為 $e^{-2/3} \approx 0.5134$