Memoryless
The exponential distribution often arises, in practice, as being the
distribution of the amount of time until some specific event occurs. For
instance, the amount of time (starting from now) until an earthquake occurs, or
until a new war breaks out, or until a telephone call you receive turns out
to be a wrong number are all random variables that tend in practice to have
exponential distributions.
We say that a nonnegative random variable X is memoryless if
If we think of X as being the lifetime of some instrument, Equation (5.1)
states that the probability that the instrument survives for at least s+thours, given that it has survived t hours, is the same as the initial
probability alive at age t, the distribution of the remaining amount of time
that it survives is the same as the original lifetime distribution (that is, it
is as if the instrument does not remember that it has already been in use for
a time t)
The condition (5.1) is equivalent to
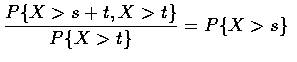
or
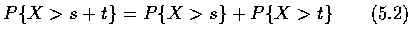
Since Equation (5.2) is satisfied when X is exponentially distributed (for
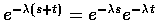 ), it follows that
exponentially distributed random variables are memoryless.
), it follows that
exponentially distributed random variables are memoryless.
Suppose that X is memoryless and let
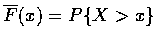 .
Then, by
Equation (5.2), it follows that
.
Then, by
Equation (5.2), it follows that
That is,
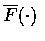 satisfies the functional equation
satisfies the functional equation
g(s+t)=g(s)g(t)
However, it turns out that only right continuous solution of this functional
equation is
and, since a distribution function is always right continuous, we must have
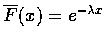
or
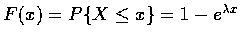
which shows that X is exponentially distributed.
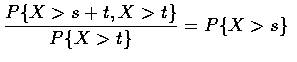 or
or
![]() .
Then, by
Equation (5.2), it follows that
.
Then, by
Equation (5.2), it follows that