Exponential Random Variables
設 X 為一連續隨機變數, 若其機率密度函數為
其中
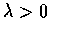 為一常數, 則稱 X 為參數是
為一常數, 則稱 X 為參數是 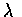 的指數隨機變數
(exponential random variable). 指數隨機變數的累積分布函數為
注意到
的指數隨機變數
(exponential random variable). 指數隨機變數的累積分布函數為
注意到
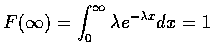 .
.
- Example
- 設 X 為參數是
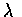 的指數隨機變數. 求 (a) E[X], 和 (b) Var(X)
的指數隨機變數. 求 (a) E[X], 和 (b) Var(X) - Solution:
- (a)
因為密度函數為
所以,
![$E[X] = \displaystyle\int_0^\infty x\lambda e^{-\lambda x}dx $](img7.gif) 利用部分積分
利用部分積分
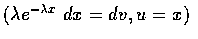 得
(b)
得
(b)
欲得 X 的變異數, 我們先求 E[X2] 利用部分積分
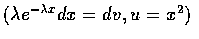 得
因此,
得
因此,
- Example
- 假設一通電話的通話時間 (單位:分鐘) 為參數是
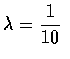 的指數隨機變數. 若某人正好在你之前到達公共電話亭,
求 (a) 你必須等 10 分鐘以上的機率為多少?
(b) 你必須等 10 到 20 分鐘的機率為多少 ?
的指數隨機變數. 若某人正好在你之前到達公共電話亭,
求 (a) 你必須等 10 分鐘以上的機率為多少?
(b) 你必須等 10 到 20 分鐘的機率為多少 ?
- Solution:
- 令 X 表示在電話亭內的人的通話的時間, 則所求的機率分別為:
(a)
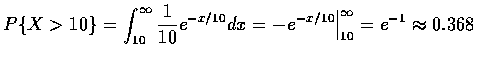
(b)
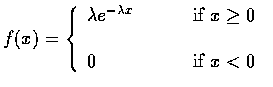
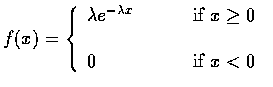
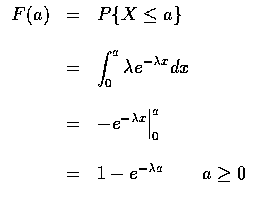
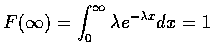 .
.
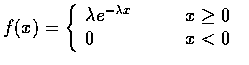
![$E[X] = \displaystyle\int_0^\infty x\lambda e^{-\lambda x}dx $](img7.gif) 利用部分積分
利用部分積分
![$\begin{array}{rcl}
E[X]&=&\displaystyle-xe^{-\lambda x}\Big \vert _0^\infty+\in...
...\vert _0^\infty \\ \\
& = & \displaystyle\frac{1}{\lambda } \\ \\
\end{array}$](img9.gif)
![$E[X^2] =\displaystyle\int_0^\infty x^2 \lambda e^{-\lambda x}dx $](img10.gif)
![$\begin{array}{rcl}
E[X^2]&=&\displaystyle-x^2e^{-\lambda x}\Big \vert _0^\infty...
...c{2}{\lambda } E[X] \\ \\
& = & \displaystyle\frac{2}{\lambda ^ 2}
\end{array}$](img12.gif)
![$Var(X) = \displaystyle\frac{2}{\lambda ^2} - \left (
\frac{1}{\lambda } \right )^2 = \frac{1}{\lambda ^2} \qquad\rule[0.02em]{1.0mm}{1.5mm}$](img13.gif)
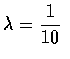 的指數隨機變數. 若某人正好在你之前到達公共電話亭,
求 (a) 你必須等 10 分鐘以上的機率為多少?
(b) 你必須等 10 到 20 分鐘的機率為多少 ?
的指數隨機變數. 若某人正好在你之前到達公共電話亭,
求 (a) 你必須等 10 分鐘以上的機率為多少?
(b) 你必須等 10 到 20 分鐘的機率為多少 ?
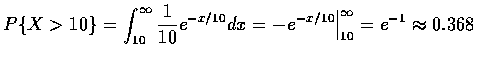
![$\begin{array}{rcl}
P\{10 < X < 20 \}&=&\displaystyle\int_{10}^{20} \frac{1}{10}...
...} - e^{-2} \\ \\
&\approx& 0.233 \qquad\rule[0.02em]{1.0mm}{1.5mm}
\end{array}$](img17.gif)