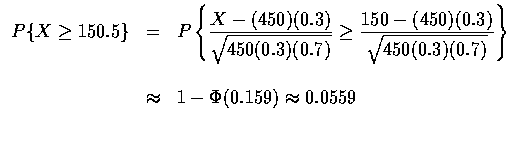The Normal Approximation to the Binomial Distribution

The DeMoiver-Laplace Limit Theorem
令 Sn 表示在每次成功機率均為 p 的 n 次獨立試驗中成功的次數, 則對任意 a < b, 且當 $ n \rightarrow \infty $ 時,

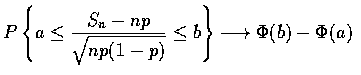
$P \left \{ a \leq \displaystyle\frac{S_n-np}{\sqrt{np(1-p)} } \leq b \right \} \longrightarrow \Phi (b) - \Phi (a) $

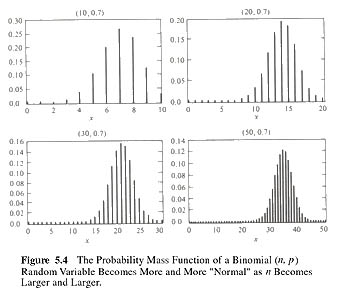
到目前為止, 對二項機率我們有兩種可能的近似值 : 卜瓦松近似和常態近似. 一般 而言, 當 n 很大且 np 適度大小時, 卜瓦松近似可得很好的近似值 ; 而當 np(1-p) 很大時, 常態近似值是相當令人滿意的.

Example
丟一公正銅板 40 次, 令 X 表示出現正面的次數. 求 X = 20的機率. 利用常態近似的方法, 然後再將它與正確的解作比較.
Solution:
因為二項隨機變數是離散型而常態隨機變數是連續型的, 故所求機率的最佳近似值為
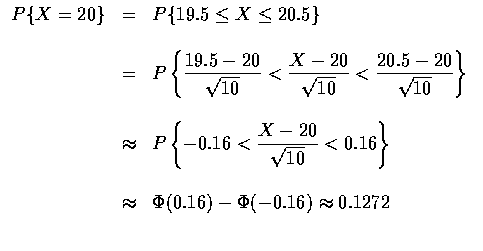
$\begin{array}{rcl} P\{X=20\} & = & P\{19.5 \leq X \leq 20.5\} \\ \\ & = & P \l... ...\\ \\ & \approx & \Phi (0.16) - \Phi (-0.16) \approx 0.1272 \\ \\ \end{array}$

而正確的解為 $P\{X=20\}=\displaystyle{40\choose 20}\left (\frac{1}{2}\right )^40 \approx 0.1254\qquad\rule[0.02em]{1.0mm}{1.5mm}$

Example
某大學一年級的理想學生數為 150 人, 該大學依過去的經驗知在被通知入學的學生中, 僅有 30% 會到校註冊入學. 現該校接受 450 位同學的入學申請, 求到校註冊的大一學生會超過 150 人的機率為多少 ?
Solution:
令 X 表示到校註冊的學生數; 則 X 為參數是 n = 450 和 p =0.3 的二項隨機變數. 其常態近似值為
$\begin{array}{rcl} P\{X \geq 150.5\}&=&P \left \{ \displaystyle\frac{X-(450)(0.... ...} \right \} \\ \\ &\approx& 1 - \Phi (0.159) \approx 0.0559 \\ \\ \end{array}$
因此接受 450 位同學的入學申請, 而實際會多於 150 位來註冊入學的機率小 於 0.06.          $\rule[0.02em]{1.0mm}{1.5mm}$