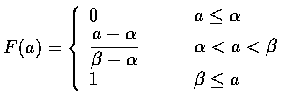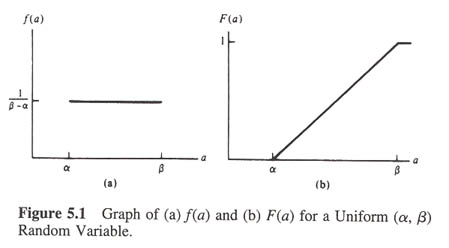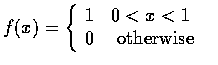
The Uniform Random Variable

若一隨機變數的機率密度函數為

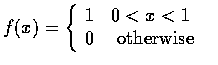
$ f(x) = \left \{ \begin{array}{ll} 1 & 0 < x < 1 \\ 0 & \mbox{ otherwise } \end{array} \right .$

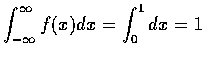則稱此隨機變數為在區間 (0,1) 上均勻分布(uniformly distributed) 的隨機 變數. 在上式中, 因 $f(x) \geq 0$ 且 $ \displaystyle\int_{-\infty}^\infty f(x)dx = \displaystyle \int_0^1dx = 1 $, 故為一密度函數. 因為只有在 $x \in (0,1) $ 時, f(x) 才大 於 0, 所以 X 的可能值必定在 (0,1)中. 又因為 f(X) 在 (0,1) 間為一常數 , 故得 X 在 (0,1) 中任一點附近的可能性都是一樣的. 欲檢查此結果, 注意到對 任意 0<a<b<1,

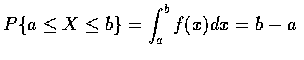
$ P\{a\leq X \leq b\} = \displaystyle\int_a^b f(x)dx = b-a $
換句話說, X 在 (0,1) 的任意子區間的機率等於該子區間的長度. 一般而言, 當 X 的機率密度函數為
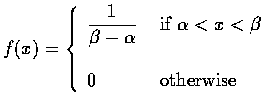
$ f(x) = \left \{ \begin{array}{ll} \displaystyle\frac{1}{\beta - \alpha} & \mbox{ if } \alpha < x < \beta \\ \\ 0 & \mbox{ otherwise } \end{array} \right . $
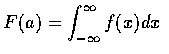則稱 X 為在區間 $(\alpha, \beta )$ 上的均勻隨機變數 (uniform random variable). 因 $F(a) = \displaystyle\int_{- \infty}^\infty f(x)dx $, 從上式可得知在區間 $(\alpha, \beta )$ 上之均勻隨機變數的分布函數為
$ F(a) = \left \{ \begin{array}{ll} 0 & \qquad a \leq \alpha \\ \displaystyle\f... ... & \qquad \alpha < a < \beta \\ 1 & \qquad \beta \leq a \end{array} \right . $
下圖, 分別表示 f(a) 和 F(a) 的圖形.