Proposition

Proposition
若 X 為一連續隨機變數, 其機率密度函數為 f(x), 則對任意 實數值函數 (real-valued function) g

$E[g(x)] = \displaystyle\int_{-\infty }^\infty g(x)f(x)dx $
Proof:
對任意非負函數 g, 根據底下的 Lemma 1 得
$\begin{array}{rcl} E[g(X)] & = & \displaystyle\int_0^\infty P\{g(X)>y\}dy \\ \\... ...int \limits_{x:g(x)>0} g(x)f(x)dx \qquad\rule[0.02em]{1.0mm}{1.5mm} \end{array}$


Lemma 1
對任一非負的隨機變數 Y, $E[Y] = \displaystyle\int_0^\infty P\{Y>y\} dy$
Proof:
設其機率密度函數為 fy, 則得

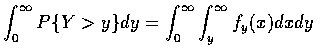
$\displaystyle\int_0^\infty P\{Y>y\}dy=\int_0^\infty\int_y^\infty f_y(x)dxdy$
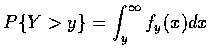其中我們使用了 $P\{Y>y\} = \displaystyle\int_y^\infty f_y(x)dx $ 的結果. 交換上式等式中的積分次得
$\begin{array}{rcl} \displaystyle\int_0^\infty P\{Y>y\}dy&=&\int_0^\infty\left (... ...nfty xf_y(x)dx \\ \\ & = & E[Y] \qquad\rule[0.02em]{1.0mm}{1.5mm} \end{array} $


Corollary 1
若 a 和 b 均為常數, 則 E[aX+b] = aE[X] + b
Proof:
系 2.1 對連續隨機變數的證明和對離散隨機變數的證明是一樣的, 唯一的不同點 是將和以積分取代, 機率質量函數以機率密度函數取代.
連續隨機變數之變異數的定義方式也和離散情形的定義方式完全一樣. 亦即, 若 X為連續隨機變 數, 其 期望值為 $\mu $, 則 X 的變異數定義(對任意類型的隨機 變數)為 $Var(X) = E[(X-\mu )^2] $
利用與離散情形同樣的方法, 可得變異數的另一個公式為

$Var(X)=E[X^2]-(E[X])^2\qquad\rule[0.02em]{1.0mm}{1.5mm}$


Example
設 X 為例 a 中的隨機變數, 試求 Var(X).
Solution:
首先求 E[X2].
$\begin{array}{rcl} E[X^2] & = & \displaystyle\int_{- \infty }^\infty x^2f(x)dx ... ...\displaystyle\int_0^1 2x^3dx \\ \\ & = & \displaystyle\frac{1}{2} \end{array}$

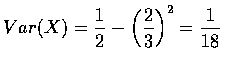
又因 $E[X] = \displaystyle\frac{2}{3}$, 故得 $Var(X)=\displaystyle\frac{1}{2}-\left ( \frac{2}{3} \right )^2=\frac{1}{18}$

仿照離散隨機變數的證明方式, 可證得對任意常數 a 和 b
         $Var(aX+b) = a^2Var(X)\qquad\rule[0.02em]{1.0mm}{1.5mm}$