Continuous Random Variables

前一章討論的離散隨機變數, 其所有可能值為有限或可數無窮多的隨機變數, 當然, 也存在一些隨機變數, 它們的所有可能值的集合是 不可數的(uncountable). 例如火車到達某一站的時間或電晶體的使用壽命 ... 等. 令 X 為這種隨機變數, 若存在一個定義在所有實數 $x \in (- \infty, \infty )$ 上的非負函數 f, 且對任意實數集合 B 滿足

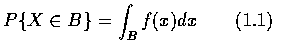
$P\{X\in B\}=\displaystyle\int_B f(x)dx\qquad (1.1)$
則稱 X 為連續隨機變數 (continuous random variable). 函數 f 稱為隨機變數 X的機率密度函數 (probability density function).

上式敘述 X 之可能值會在 B 中的機率可由機率密度函數在 B 上積分而得. 因為 X 的值必定是某一實數, 所以 f 必需滿足

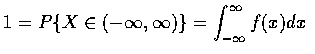
$1=P\{X\in (-\infty,\infty)\}=\displaystyle\int_{-\infty}^\infty f(x)dx$

所有有關 X 的機率敘述, 都可由 f 得到. 例如, 當 B = [a,b] 時, 我們可由 (1.1)式得

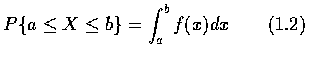
$P\{a\leq X\leq b\}=\displaystyle\int_a^b f(x)dx\qquad (1.2)$

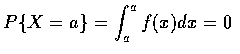
在 (1.2) 式中, 若令 a=b, 則得 $P\{X=a\}=\displaystyle\int_a^a f(x)dx=0$

也就是說, 若 X 為一連續隨機變數, 則 X 等於任一 個固定值的機率為 0. 因此, 對連續隨機變數而言, 我們有

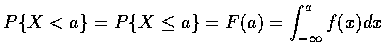
$P\{X<a\}=P\{X\leq a\}=F(a)=\displaystyle\int_{- \infty}^a f(x)dx$

Example
電腦在故障之前的使用時間 (單位 : 小時) 為一連續隨機變數, 其機率密度函數為
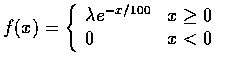
$f(x) = \left\{ \begin{array}{lr} \lambda e^{-x/100} & x \geq 0 \\ 0 & x<0 \\ \end{array}\right .$
(a) 試求電腦在故障之前使用時間介於 50 與 150 小時之間的機率為多少 ?
(b) 使用時間少於 100 小時的機率為多少 ?
Solution:
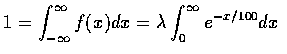
(a) 因, $1 = \displaystyle\int_{-\infty}^\infty f(x)dx = \lambda \int_0^\infty e^{-x/100} dx $
所以, $1 = - \lambda(100)e^{-x/100} \Big \vert _0^\infty = 100 \lambda $
故, 電腦在故障前使用時間介於 50 和 150 小時之間的機率為
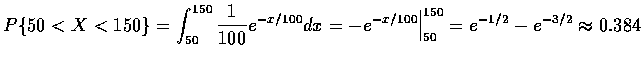
$P\{50<X<150\} = \displaystyle\int_{50}^{150}\frac{1}{100} e^{-x/100} dx = -e^{-x/100} \Big \vert _{50}^{150} = e^{-1/2} - e^{-3/2} \approx 0.384 $

(b) 同理可得
$P\{X<100\}=\displaystyle\int_0^{100}\frac{1}{100} e^{-x/100} dx = -e^{-x/100} \Big \vert _0^{100} = 1 - e^{-1} \approx 0.633\qquad\rule[0.02em]{1.0mm}{1.5mm}$