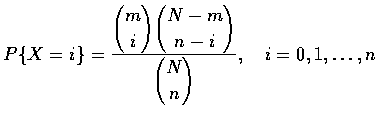
The Hypergeometric Random Variable

設袋中有 N 個球, 其中有 m 個白球, N-m 個黑球. 假設自袋中隨機取出 (不放回) n 個球. 若令 X 表示取出的白球個數, 則

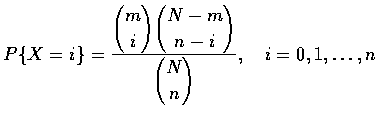
$P\{X=i\}=\displaystyle{{\displaystyle{m\choose i}{N-m\choose n-i}}\over\displaystyle{N\choose n}}, \quad i=0,1,\ldots,n$
對任一隨機變數 X, 若對某些 n,N,m 的值其機率質量函數如上式, 則稱 X 為 超幾何隨機變數(hypergeometric random variable).

Example
設 X 為一超幾何隨機變數, 其參數為 n,N,m. 試求 X 的期望值和變異數.
Solution:
$\begin{array}{rcl} E[X^k]&=&\displaystyle\sum_{i=10}^n i^k P\{X=i\} \\ \\ &=&\... ...yle\sum_{i=1}^n{m\choose i}{N-m \choose n-i}\Big /{N \choose n} \\ \end{array}$

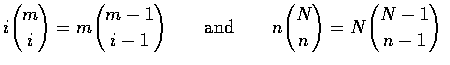因為 $i\displaystyle{m\choose i}=m{m-1\choose i-1}\qquad\mbox{and}\qquad n{N\choose n} =N{N-1\choose n-1}$所以,

$\begin{array}{rcl} E[X^k]&=&\displaystyle\frac{mn}{N}\sum_{i=1}^ni^{k-1}{m-1\ch... ...N-1 \choose n-1} \\ \\ &=&\displaystyle\frac{nm}{N}E[(Y+1)^{k-1}] \end{array} $
其中 Y 為一超幾何隨機變數, 其參數為 n-1,N-1,m-1. 因此, 令 k=1 得 $E[X]=\displaystyle\frac{nm}{N}$

若從含有 m 個白球的 N 個球中隨機取出 n 個球, 則取出之白球的期望數為 $\displaystyle\frac{nm}{N}$. 在 E[X2] 的式子中, 令 k=2 得

$\begin{array}{rcl} E[X^2]&=&\displaystyle\frac{nm}{N}E[(Y+1)] \\ \\ &=&\displaystyle\frac{nm}{N}\left [\frac{(n-1)(m-1)}{N-1}+1\right ] \\ \end{array}$

最後一個等式利用剛剛得到的結果來求超幾何隨機變數 Y 的期望值. 因 $E[X]=\displaystyle\frac{nm}{N}$, 我們得

$Var(X)=\displaystyle\frac{nm}{N}\left [\frac{(n-1)(m-1)}{N-1}+1-\frac{nm}{N}\right ]$

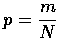若令 $p=\displaystyle\frac{m}{N}$ 表示白球的比例, 由上式可得

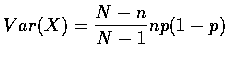
$Var(X)=\displaystyle\frac{N-n}{N-1}np(1-p)$

當 N 比 n 大出很多時 ( 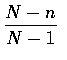$\displaystyle\frac{N-n}{N-1}$ 趨近於 1) 則 $Var(X)\approx np(1-p)\qquad\rule[0.02em]{1.0mm}{1.5mm}$