The Geometric Probability Distributions

假設進行一序列的獨立試驗直到第一次成功為止, 其中每次試驗成功的機率均為 p,0<p<1. 若我們令 X 等於所需的試驗次數, 則

$P\{X=n\}=(1-p)^{n-1}p\qquad n=1,2,\ldots$
因為 X 等於 n 的充要條件為首 n-1 次試驗都失敗, 而第 n 次試驗成功. 又因連續試驗的結果是互相獨立的, 所以可以求得上式.

又因為

$\displaystyle\sum_{n=1}^\infty P\{X=n\}=p\sum_{n=1}^\infty (1-p)^{n-1}= \frac{p}{1-(1-p)}=1$
所以此試驗"成功"會發生的機率為 1.

設 X 為一隨機變數, 若 X 的機率質量函數如最上式所示, 則稱 X 為參數是 p 的幾何隨機變數(geometric random variable).

Example
袋中有 N 個白球和 M 個黑球. 每次自袋中隨機取出一球, 直到取到黑球為止. 若我們假設取出的球在下次取球前要放回袋中, 試求 (a)恰需取 n 次和 (b)至少需要取 k 次的機率分別是多少?
Solution:
令 X 表示取到一個黑球所需的次數, 則 X 滿足 第一式, 其中 p=M/(M+N). 因此
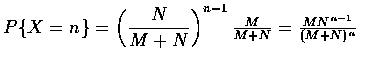
(a) $P\{X=n\}=\left (\displaystyle\frac{N}{M+N}\right )^{n-1} \frac{M}{M+N}=\frac{MN^{n-1}}{(M+N)^n}$
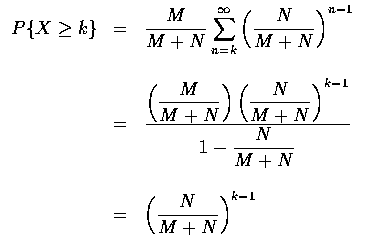
(b) $\begin{array}{rcl} P\{X\geq k\}&=&\displaystyle\frac{M}{M+N}\sum_{n=k}^\infty\l... ...N}{M+N}} \\ \\ &=&\left (\displaystyle\frac{N}{M+N} \right )^{k-1} \end{array}$
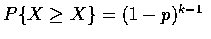
Of course, (b) could have been obtained directly, since the probability that at least k trials are necessary to obtain a success is equal to the probability that the first k-1 trials are all failures. That is, for a geometric random variable $P\{X\geq X\}=(1-p)^{k-1}$          $\rule[0.02em]{1.0mm}{1.5mm}$

Example
求幾何隨機變數的期望值.
Solution
令 q=1-p, 則我們得
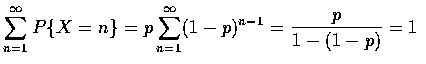
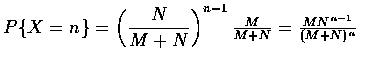
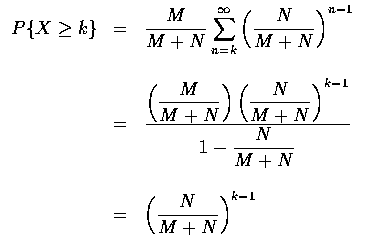
$\begin{array}{rcl} E[X]&=&\displaystyle\sum_{n=1}^\infty nq^{n-1}p \\ \\ &=&p\... ...\\ \\ &=&\displaystyle\frac{1}{p}\qquad\rule[0.02em]{1.0mm}{1.5mm} \end{array}$

Example
求幾何隨機變數的變異數.
Solution
先求 E[X2]. 令 q=1-p
$\begin{array}{rcl} E[X^2]&=&\displaystyle\sum_{n=1}^\infty n^2q^{n-1}p \\ \\ &... ...^3}\right ] \\ \\ &=&\displaystyle\frac{2}{p^2}-\frac{1}{p} \\ \\ \end{array}$
又因, $E[X]=\displaystyle\frac{1}{p}$故有, $Var(X)=\displaystyle\frac{1-p}{p^2}\qquad\rule[0.02em]{1.0mm}{1.5mm}$