Example

The preceding discussion explains why a Poisson random variable is usually a good approximation for such diverse phenomena as the following:

1.
The number of earthquakes occurring during some fixed time span.
2.
The number of wars per year.
3.
The number of electrons emitted from a heated cathode during a fixed time period.
4.
The number of deaths in a given period of time of the policyholders of a life insurance company.

Example
Suppose that earthquakes occur in the western portion of the United States in accordance with assumptions 1,2, and 3 with 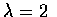$\lambda=2$ and with 1 week as the unit of time. (That is, earthquakes occur in accordance with the three assumptions at a rate of 2 per week.)
(a) Find the probability that at least 3 earthquakes occur during the next 2 weeks.
(b) Find the probability distribution of the time, starting from now, until the next earthquake.
Solution:
(a) We have
$\begin{array}{rcl} P\{N(2)\geq 3\}&=&1-P\{N(2)=0\}-P\{N(2)=1\}-P\{N(2)=2\} \\ \... ...^{-4}-4e^{-4}-\displaystyle\frac{4^2}{2}e^{-4} \\ \\ &=&1-13e^{-4} \end{array}$
(b) Let X denote the amount of time (in weeks) until the next earthquake. Because X will be greater than t if and only if no events occur within the next t units of time, we have
$P\{X>t\}=P\{N(t)=0\}=e^{-\lambda t}$
so the probability distribution function F of the random variable X is given by
$\begin{array}{rcl} F(t)=P\{X\leq t\}=1-P\{X>t\}&=&1-e^{\lambda t} \\ &=&1-e^{-2t}\qquad\rule[0.02em]{1.0mm}{1.5mm}\\ \end{array}$