Poisson Process

Let us suppose that events are indeed occurring at certain(random) points of time, and let us assume that for some positive constant $\lambda$ the following assumptions hold true:

1.
The probability that exactly 1 event occurs in a given interval of length his equal to $\lambda h + o(h)$, where o(h) stnads for any function f(h)that is such that $\displaystyle\lim_{h\rightarrow 0}f(h)/h=0$. [For instance, f(h)=h2 is o(h), whereas f(h)=h is not.]
2.
The probability that 2 or more events occur in an interval of length h is equal to o(h).
3.
For any integers $n,j_1,j_2,\ldots ,j_n$, and any set of n nonoverlapping intervals, if we define Ei to be the event that exactly ji of the events under consideration occur in the ith of these intervals, then events $E_1,E_2,\ldots ,E_n$ are independent.

Loosely put, assumptions 1 and 2 state that for small values of h, the probability that exactly 1 event occurs in an interval of size h equals $\lambda h$ plus something that is small compared to h, whereas the probability that 2 or more events occur is small compared to h. Assumption 3 states that whatever occurs in one interval has no (probability) effect on what will occur in other nonoverlapping intervals.

Under assumptions 1,2, and 3, we shall now show that the number of events occurring in any interval of length t is a Poisson random variable with parameter $\lambda t$. To be precise, let us call the interval [0,t] and denote by N(t) the number of events occurring in that interval. To obtain an expression for $P\{N(t)=k\}$, we start by breaking the interval [0,t] into n nonoverlapping subintervals each of length t/n as follow.

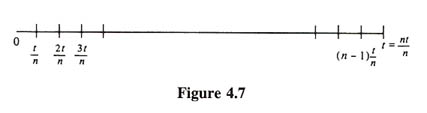
Now,

$\begin{array}{rcl} P\{N9t)=k\}&=&P\{k\mbox{ of the n subintervals contain exact... ...terval contains}\\ &&\mbox{ 2 or more events}\} \qquad (8.2)\\ \\ \end{array}$

This follows because the event on the left side of Equation (8.2), that is, $\{N(t)=k\}$, is clearly equal to the union of the two mutually exclusive events on the right side of the equation. Letting A and B denote the two mutually exclusive events on the right side of Equation (8.2), we have

$\begin{array}{rcl} P(B)&=&P\{\mbox{at least one subinterval contains 2 or more ... ...ght ) \\ \\ &=&t\left [\displaystyle\frac{o(t/n)}{t/n}\right ] \\ \end{array}$

Now, for any t, $t/n\rightarrow\infty$ as $n\rightarrow\infty$ and so $o(t/n)/(t/n)\rightarrow\infty$ as $n\rightarrow\infty$ by the definition of o(h). Hence

$P(B)\rightarrow 0$ as $n\rightarrow\infty\qquad (8.3)$

On the other hand, since assumptions 1 and 2 imply that $P\{0\mbox{ events occur in an interval of length } h\}$
$=1-[\lambda h+o(h)+o(h)]=1-\lambda h-o(h)$
we see from the independence assumption, number 3, that

$\begin{array}{rcl} P(A)&=&P\{k\mbox{ of the subintervals contain exactly 1 even... ...bda t}{n}\right )- o\left (\frac{t}{n}\right )\right ]^{n-k} \\ \\ \end{array}$

However, since

$n\left [\displaystyle\frac{\lambda t}{n}+o\left (\frac{t}{n}\right )\right ]= \... ...{o(t/n)}{t/n}\right ]\rightarrow\lambda t \qquad \mbox{ as } n\rightarrow\infty$
in follows, by the same argument that verified the Poisson approximation to the binomial, that
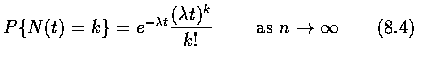
$P\{N(t)=k\}=e^{-\lambda t}\displaystyle\frac{(\lambda t)^k}{k!}\qquad \mbox{ as }n\rightarrow\infty\qquad (8.4)$

Thus, from Equations (8.2), (8.3), (8.4), we obtain, by letting $n\rightarrow\infty$,

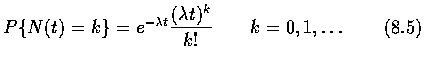
$P\{N(t)=k\}=e^{-\lambda t}\displaystyle\frac{(\lambda t)^k}{k!} \qquad k=0,1,\ldots\qquad (8.5)$

Hence, if assumptions 1,2, and 3 are satisfied, the number of events occurring in any fixed interval of length t is a Poisson random variable with mean $\lambda t$; and we say that the events occur in accordance with a Poisson process having rate $\lambda$. The value $\lambda$, which can be shown to equal the rate per unit time at which events occur, is a constant that must be empirically determined.