The Poisson Random Variable
設 X 為一隨機變數, 其所有可能值為
![]() ,
若對某一
,
若對某一
![]() ,
,
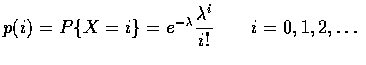
因此 probability mass function 為,
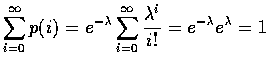
因為卜瓦松隨機變數可以作為參數是 (n,p) 之二項隨機變數在 n 很大, p很小且 np 適度大小之情況下的近似值, 所以其應用的範圍相當的廣泛.
欲知此近似的情況, 我們設 X 為參數是 (n,p) 的二項隨機變數,
且令
![]() .
則
.
則
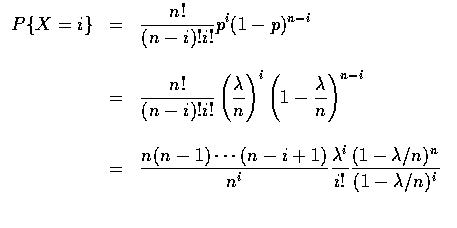
對 n 很大, ![]() 適度大小時, 則
適度大小時, 則
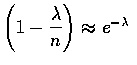
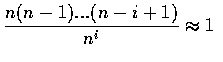
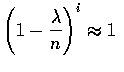
因此, 當 n 很大且 ![]() 適度大小時,
適度大小時,
![]()
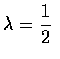 的卜瓦松隨機變數. 試求本頁上至少有一個錯誤的機率.
的卜瓦松隨機變數. 試求本頁上至少有一個錯誤的機率.