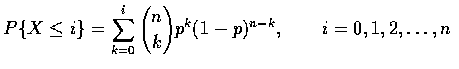
Computing the Binomial Distribution Function

設 X 為參數是 (n,p)的二項隨機變數. 計算其分布函數

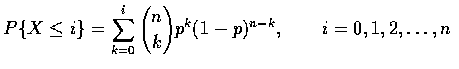
$P\{X\leq i\}=\displaystyle\sum_{k=0}^i{n\choose k}p^k(1-p)^{n-k}, \qquad i=0,1,2,\ldots ,n$
的關鍵在於使用下述 $P\{X=k+1\}$ 及 $P\{X=k\}$ 間的關係式:
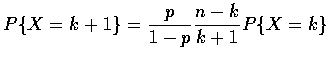
$P\{X=k+1\}=\displaystyle\frac{p}{1-p}\frac{n-k}{k+1}P\{X=k\}$

Example
令 X 為一二項隨機變數, 其參數為 n=6, p=0.4. 然後從 $P\{X=0\}=(0.6)^6$ 開始, 遞迴地使用上式, 得
$\begin{array}{rcl} P\{X=0\}&=&(0.6)^6 \approx 0.0467 \\ \\ P\{X=1\}&=&\display... ...}{66}P\{X=5\}\approx 0.0041 \qquad\rule[0.02em]{1.0mm}{1.5mm}\\ \\ \end{array}$

To compute $P\{X\leq i\}$ the program should compute first $P\{X=i\}$ and then use the recursion the compute successively $P\{X=i-1\}$, $P\{X=i-2\}$, and so on. The computation of

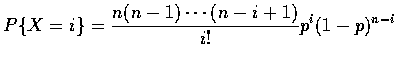
$P\{X=i\}=\displaystyle\frac{n(n-1)\cdots (n-i+1)}{i!}p^i(1-p)^{n-i}$

can be accomplished by first taking logrithms to obtain

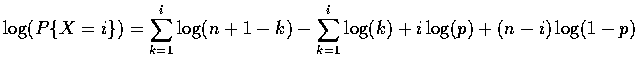
$\displaystyle\log(P\{X=i\})=\sum_{k=1}^i\log(n+1-k)-\sum_{k=1}^i\log(k)+ i\log(p)+(n-i)\log(1-p)$

and then taking $P\{X=i\}=\exp\{log(P\{X=i\})\}$