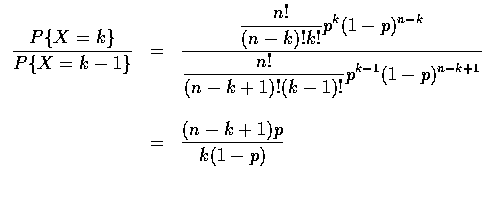Properties of Binomial Random Varables

二項隨機變數的性質
We will now examine the properties of a binomial random variable with parameters n and p. To begin, let us compute its expected and variance.

$\begin{array}{rcl} E[X^k]&=&\displaystyle\sum_{i=0}^ni^k{n\choose i}p^i(1-p)^{n... ...\ &=&\displaystyle\sum_{i=1}^ni^k{n\choose i}p^i(1-p)^{n-i} \\ \\ \end{array}$

And

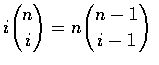
$i\displaystyle{n\choose i}=n{n-1\choose i-1}$
$\begin{array}{rcl} E[X^k]&=&np\displaystyle\sum_{i=1}^ni^{k-1}{n-1\choose i-1}p... ...)^{n-1-j} \quad(\mbox{ Let }j=i-1)\\ \\ &=&npE[(Y+1)^{k-1}] \\ \\ \end{array}$

其中 Y 為參數是 (n-1,p) 的二項隨機變數. 在上式中, 令 k=1, 得 E[X] = np. 也就是說, 在成功機率為 p 之 n 次獨立試驗中, 成功的期望次數為 np. 在上式公式中, 令 k=2 且利用剛得到的二項隨機變數之期望值的公式得

E[X2]=npE[(Y+1)]=np[(n-1)p+1]
因 E[X]=np, 所以
$\begin{array}{rcl} Var(X)&=&E[X^2]-(E[X])^2 \\ \\ &=&np[(n-1)p+1]-(np)^2 \\ \\ &=&np(1-p) \end{array}$

Proposition
由上面的討論可以整理出, 若 X 為一參數是 (n,p) 的二項隨機變數, 則

E[X]=np
Var(X)=np(1-p)

Proposition
設 X 為一參數是 (n,p) 的二項隨機變數, 其中 0<p<1, 那麼當 k 從 0 增加到 n 時, $P\{X=k\}$ 先單調遞增(increases monoton-ically), 且當 k 為小於或等於 (n+1)p 的最大整數時, $P\{X=k\}$ 為最大.
Proof:
考慮 $P\{X=k\}/P\{X=k-1\}$, 且決定當 k 為何值時, 它大於或小於 1.

$\begin{array}{rcl} \displaystyle\frac{P\{X=k\}}{P\{X=k-1\}}&=&\displaystyle\fra... ...1-p)^{n-k+1}} \\ \\ &=&\displaystyle\frac{(n-k+1)p}{k(1-p)} \\ \\ \end{array}$
因此, $P\{X=k\}\geq P\{X=k-1\}$ 若且唯若 $(n-k+1)p\geq k(1-p)$ 或相當於, 若且唯若 $k \leq (n+1)p $ 故得證.         $\qed$