Example
- Example
- 丟 5 個均勻銅板. 若假設出現的結果互相獨立, 試求出現正面個數的機率質量函數.
- Solution:
- 令 X 表示出現正面 ("成功") 的個數, 則 X 是參數為
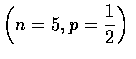 的二項隨機變數. 因此, 由上式得
的二項隨機變數. 因此, 由上式得
- Example
- 假設人的某一特徵 (如眼睛的顏色或左撇子) 是根據一對基因來分類的,
且假設 d 代表顯性因子而 r 代表隱性因子. 因此某人有 dd 基因是純顯性的,
有 rr 基因是純隱性的, 而有 rd 基因則是混合性的.
純顯性和混合性在外觀上是相同的. 孩子從父母各得一個因子. 對某一特徵而言,
若兩位都是混合性的父母有 4 個小孩,
試求 4 個小孩中有 3 個小孩具有顯性基因之外觀的機率為多少?
- Solution:
- 如果我們假設每個小孩從他父親或母親那兒繼承兩個因子中之任一的機會是均等的.
則雙親都是混合性的小孩有 dd , rr 或 rd 對基因的機率分別是
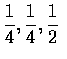 .
因為當基因對是 dd 或 rd 時,
後代將會有顯性基因的外觀, 因此這種小孩的個數是參數為
.
因為當基因對是 dd 或 rd 時,
後代將會有顯性基因的外觀, 因此這種小孩的個數是參數為
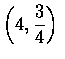 的二項隨機變數. 故得所求的機率為
的二項隨機變數. 故得所求的機率為
- Example
- 某法院陪審團由 12 位成員所組成. 若其中有 8 人或 8 人以上認為被告有罪,
則被告將被宣判有罪. 假設每位成員獨立審判,
且設每位成員作出正確判決的機率為
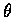 ,
試求陪審團作出正確判決的機率為多少?
,
試求陪審團作出正確判決的機率為多少?
- Solution:
- 此問題無解, 因為所給的條件不夠. 如果說被告是無辜的, 則陪審團作出正確判決的機率為
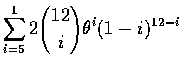 .
然而, 當被告有罪時,
正確判決的機率為
.
然而, 當被告有罪時,
正確判決的機率為
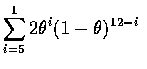 .
因此,
若以
.
因此,
若以  表示被告有罪的機率, 則以他是否有罪作為條件,
我們得到陪審團將做出正確判決的機率為
表示被告有罪的機率, 則以他是否有罪作為條件,
我們得到陪審團將做出正確判決的機率為
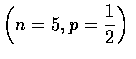 的二項隨機變數. 因此, 由上式得
的二項隨機變數. 因此, 由上式得
![$\begin{array}{rcccl}
P\{X=0\}&=&\displaystyle{5\choose 0}\left (\frac{1}{2}\rig...
...ht )^0&=&\displaystyle\frac{1}{32}\qquad\rule[0.02em]{1.0mm}{1.5mm}
\end{array}$](img2.gif)
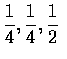 .
因為當基因對是 dd 或 rd 時,
後代將會有顯性基因的外觀, 因此這種小孩的個數是參數為
.
因為當基因對是 dd 或 rd 時,
後代將會有顯性基因的外觀, 因此這種小孩的個數是參數為
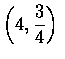 的二項隨機變數. 故得所求的機率為
的二項隨機變數. 故得所求的機率為
![$\displaystyle{4\choose 3}\left (\frac{3}{4}\right )^3\left (\frac{1}{4}\right )^1=
\frac{27}{64}\qquad\rule[0.02em]{1.0mm}{1.5mm}$](img5.gif)
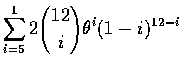 .
然而, 當被告有罪時,
正確判決的機率為
.
然而, 當被告有罪時,
正確判決的機率為
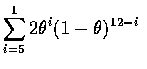 .
因此,
若以
.
因此,
若以 ![$\alpha\displaystyle\sum_{i=8}^12\theta^i(1-\theta )^{12-i}+(1-\alpha)
\sum_{i=5}^12{12\choose i}\theta^i(1-\theta)^{12-i}\qquad\rule[0.02em]{1.0mm}{1.5mm}$](img10.gif)
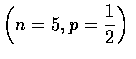 的二項隨機變數. 因此, 由上式得
的二項隨機變數. 因此, 由上式得
![$\begin{array}{rcccl}
P\{X=0\}&=&\displaystyle{5\choose 0}\left (\frac{1}{2}\rig...
...ht )^0&=&\displaystyle\frac{1}{32}\qquad\rule[0.02em]{1.0mm}{1.5mm}
\end{array}$](img2.gif)
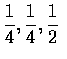 .
因為當基因對是 dd 或 rd 時,
後代將會有顯性基因的外觀, 因此這種小孩的個數是參數為
.
因為當基因對是 dd 或 rd 時,
後代將會有顯性基因的外觀, 因此這種小孩的個數是參數為
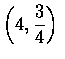 的二項隨機變數. 故得所求的機率為
的二項隨機變數. 故得所求的機率為
![$\displaystyle{4\choose 3}\left (\frac{3}{4}\right )^3\left (\frac{1}{4}\right )^1=
\frac{27}{64}\qquad\rule[0.02em]{1.0mm}{1.5mm}$](img5.gif)
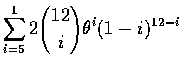 .
然而, 當被告有罪時,
正確判決的機率為
.
然而, 當被告有罪時,
正確判決的機率為
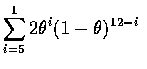 .
因此,
若以
.
因此,
若以 ![$\alpha\displaystyle\sum_{i=8}^12\theta^i(1-\theta )^{12-i}+(1-\alpha)
\sum_{i=5}^12{12\choose i}\theta^i(1-\theta)^{12-i}\qquad\rule[0.02em]{1.0mm}{1.5mm}$](img10.gif)